Глава IV. Соотношения между аркфункциями

§ 13. Соотношения первого рода

Соотношения первого рода вытекают из зависимости между тригонометрическими функциями дополнительных дуг.

Теорема. При всех допустимых значениях х имеют место соотношения:

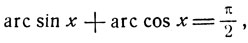
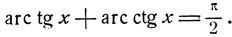
Доказательство.

Из формул тригонометрии:

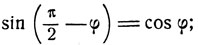
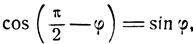
(1)

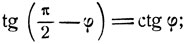
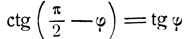
(2)

получаются соотношения, связывающие значения функции arc sin x и arc cos x. Обозначим φ = arc sin x, тогда имеем sin φ = x. На основании формул (1) получим:

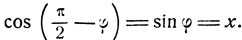
Исследуем, в каких пределах расположена дуга ^π/₂ - φ.

Так как:

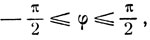
и

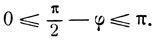
Итак, дуга

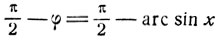
имеет косинус, равный х, и расположена на сегменте [0, π]. Но по определению арккосинуса единственная дуга на сегменте [0, π], имеющая косинус, равный х, есть arc cos x.

Следовательно, имеем

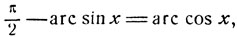
откуда

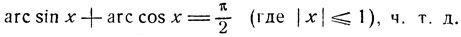
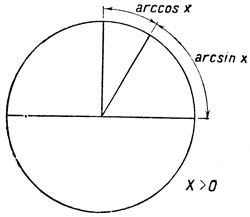
Черт. 31

На чертежах 31 и 32 дано геометрическое пояснение доказанного равенства для случаев x>0 и х<0.

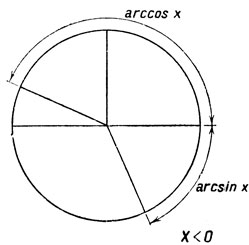
Черт. 32

Следуя указанному методу, может быть доказано тождество

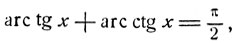
являющееся следствием формул (2), ч. т. д.