
§ 12. Примеры преобразований
Переходим к рассмотрению основных преобразований, которые могут быть получены на основе выведенных формул.
1) Преобразуем выражение: sin (2 arc sin x). Применяя формулу sin 2α = 2 sin α cos α, имеем:
sin (2 arc sin x) = 2 sin (arc sin x) cos (arc sin x) = 2x √(1-x2).
2) Подобным же образом устанавливается справедливость равенств:
cos (2 arc cos x) = cos2 (arc cos x) - sin2 (arc cos x) = 2x2 - 1;
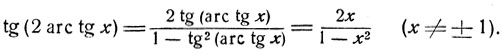
3) Пользуясь теоремой сложения и формулами предыдущего параграфа, получим:
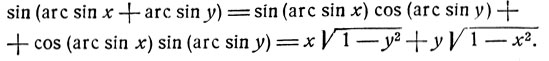
4) Следуя приему, указанному в предыдущем примере, можно доказать следующие равенства:
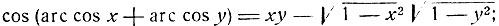
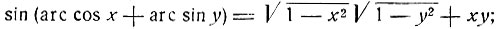
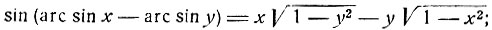
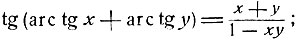
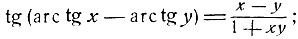
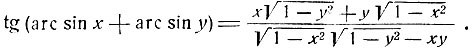
5) Из тригонометрии известно, что sin 2α и cos 2α рационально выражаются через tg α по следующим формулам:
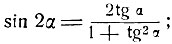
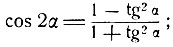
полагая в этих формулах α = arc tg x, получим:
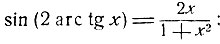
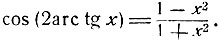
Как следовало ожидать, мы получили рациональные функции.
6) Преобразуем 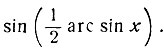 Полагая в формуле
Полагая в формуле
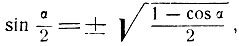
α = arc sin x, получим:
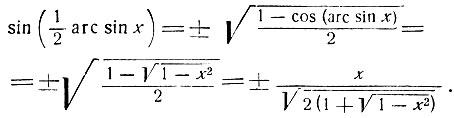
Знак выражения 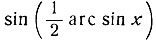 совпадает со знаком x: следовательно, перед радикалом должен быть взят знак +, так как только тогда знак правой части будет совпадать со знаком x.
совпадает со знаком x: следовательно, перед радикалом должен быть взят знак +, так как только тогда знак правой части будет совпадать со знаком x.
Итак, имеем:
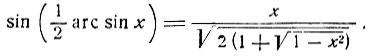
Тем же методом, доказываются равенства:
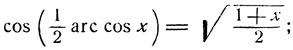
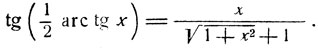
В конце настоящей главы приведен ряд примеров и упражнений на выполнение подобного рода преобразований.
Выведем формулы преобразования выражений вида sin (m arc sin x), cos (m arc cos x) и т. д., где m>0 - целое число. Воспользуемся формулами:
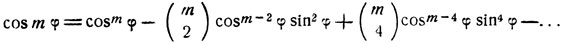
(последний член равен 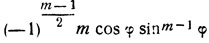 при нечетном m и
при нечетном m и 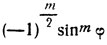 при m четном).
при m четном).
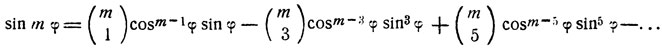
(последний член равен 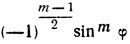 при нечетном m и
при нечетном m и 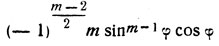 при четном m).
при четном m).
В написанных формулах символ 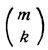 означает число сочетаний из m элементов по k.
означает число сочетаний из m элементов по k.
Формулы (1) и (2) могут быть получены, если воспользоваться известной из теории комплексных чисел формулой Моавра;

Разлагая правую часть равенства но формуле бинома Ньютона, получим:
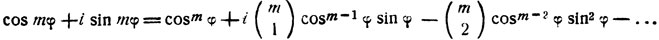
Приравнивая в этом равенстве действительную часть действительной и мнимую мнимой, получим формулы (1) и (2).
Полагая в формуле (2) φ = arc sin x и пользуясь равенством,
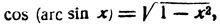
получим:
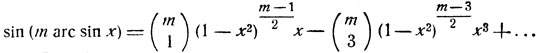
Подобным же образом, полагая в формуле (1) φ = arc cos x, будем иметь:
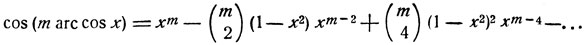
Последнее равенство показывает, что функция cos (m arc cos x), определенная в сегменте [-1, 1] (так как только в этом сегменте arc cos x имеет смысл), совпадает на этом сегменте с некоторым многочленом m-й степени. Эти многочлены носят название полиномов Чебышева, по имени великого русского ученого П. Л. Чебышева. О некоторых замечательных свойствах полиномов Чебышева сказано в специальном дополнении в конце книги.
В качестве дальнейшего примера рассмотрим tg (m arc tg x). При всяком целом m эта функция является рациональной.
В самом деле:
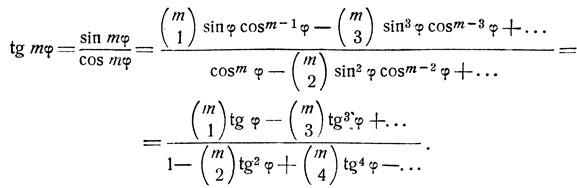
Полагая в формуле (3) φ = arc tg x, получим:
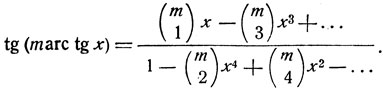
Читатель может убедиться, пользуясь выведенными выше формулами, что функции sin (m arc cos x); cos (m arc tg x); tg (m arc sin x) и пр. (m - целое число) могут быть представлены алгебраическими выражениями.
Приведенными примерами мы не исчерпали всех возможных этого рода преобразований, однако методы их выполнения выяснены достаточно подробно.
Упражнения.
1) Проверить справедливость равенств:
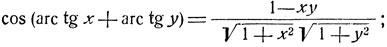
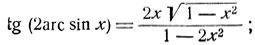
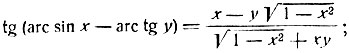
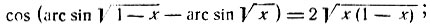
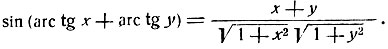
2) Доказать, что x + y + z = xyz при условии
arc tg x + arc tg y + arc tg z = π.
Решение. Воспользуемся формулой.
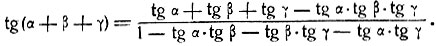
Согласно условию, имеем:
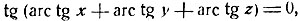
откуда
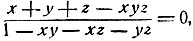
следовательно,
x + y + z = xyz.
3) Показать, что ctg [arc tg x + arc tg(1-x)] = 1 - x - x2.
4) Написать в виде многочленов:
cos (3 аrс cos x); cos (4 arc cos x).
5) Написать в виде алгебраических функций:
tg (5 аrc tg x); sin (4 arc sin x); sin (3 аrс tg x).
6) Показать, что:
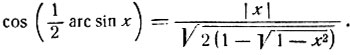
Решение. Полагая в формуле
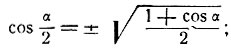
α = arc sin x,
после элементарных преобразований получим:
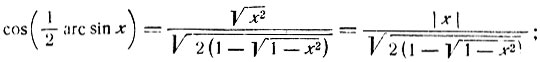
так как 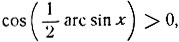 то в числителе следует взять x по абсолютной величине.
то в числителе следует взять x по абсолютной величине.
7) Показать, что
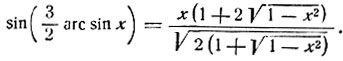
Указание: положить в формуле sin 3α = 3 sin α - 4 sin 3α, α = - arc sin x.
8) Показать, что 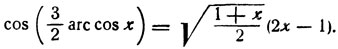
9) Доказать равенство
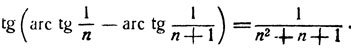
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'