Глава III. Тригонометрические операции над аркфункциями

§ 11. Основные формулы

Тригонометрические функции от одного и того же аргумента выражаются алгебраически одна через другую, поэтому в результате выполнения какой-либо тригонометрической операции над любой из аркфункций получается алгебраическое выражение.

В силу определения аркфункций:

на сегменте -1≤х≤1 и

в интервале -∞<x<∞.

Равенства (1) не являются тождествами, справедливыми при всех действительных значениях х. Так, например, при |х|>1 выражение arc sin x, а следовательно, и sin (arc sin x) теряет смысл. Итак, при |х|>1 левая часть равенства

не имеет смысла, а правая смысла не теряет, а потому говорить о выполнении равенств (1) не представляется возможным. Равенства (1) суть тождества лишь на сегменте - 1≤x≤1. На чертеже 29 графически показано различие между функциями, заданными формулами

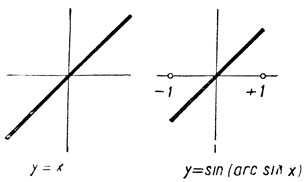
Черт. 29

Первая изображается биссектрисой координатного угла, а вторая - лишь отрезком этой биссектрисы. Равенства (2) являются тождествами, справедливыми при всех действительных значениях х.

Перейдем к более сложным преобразованиям.

1) Преобразуем выражение cos (arc sin x). Мы знаем, что косинус может быть выражен через синус по формуле

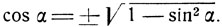
Полагая в этой формуле α = arc sin x, будем иметь sin α = x, следовательно, получим

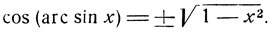
Выясним, какой из знаков должен быть взят перед радикалом. Из тригонометрии известно, что косинус дуги, заключенной на сегменте 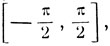положителен или равен нулю, а так как

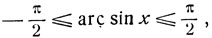
то перед радикалом следует взять знак +. Итак,

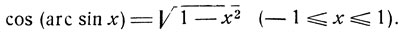
Полученному соотношению легко дать геометрическую интерпретацию. Рассмотрим тригонометрический круг (радиус, как всегда, считаем равным 1, черт. 30).

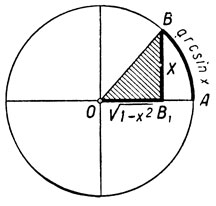
Черт. 30

Число х есть величина линии синуса ВВ₁ угла АОВ = arc sin x. Величина отрезка ОВ₁ есть значение косинуса угла AОВ:

По теореме Пифагора

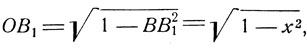
откуда:

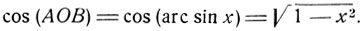
2) Подобным же образом найдем:

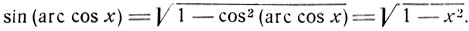
В силу неравенств 0≤ arc cjs z ≤π имеем sin (arc cos x)≥0, а поэтому перед радикалом необходимо взять знак +. Геометрический вывод предоставляем читателю.

3) Из соотношения 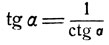следует:

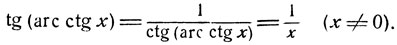
4) В качестве дальнейшего примера рассмотрим функцию tg (arc sin x); имеем:

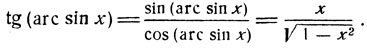
5) На основании формулы тригонометрии, выражающей синус через тангенс

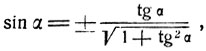
получим:

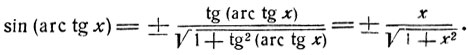
Если x<0, то sin (arc tg x)<0 и если x>0, то sin (arc tg x)>0. В правой части мы должны выбрать знак +, так как только при таком выборе знака дробь 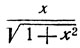будет иметь тот же знак, что и знак х.

Итак,

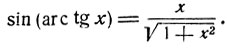
Дадим сводку формул, получающихся в результате выполнения простейших тригонометрических операций над аркфункциями. Справедливость всех этих формул может быть установлена читателем при помощи рассуждений, подобных приведенным выше.

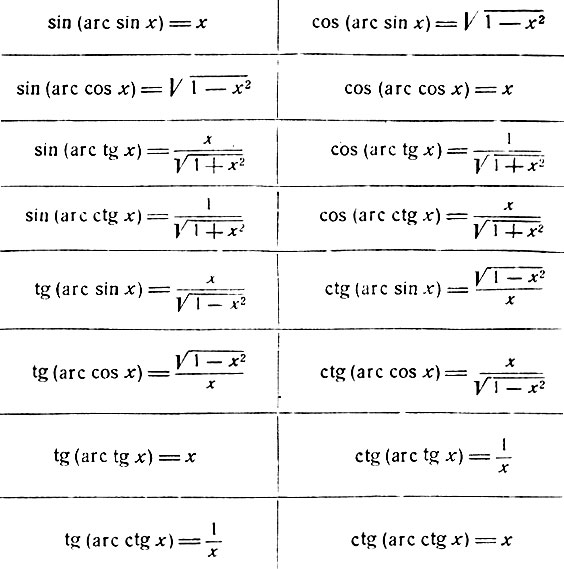
Выражения, находящиеся в правых частях каждого из написанных в таблице равенств, суть алгебраические. Эти формулы являются не чем иным, как только иначе написанными, известными из тригонометрии формулами, при помощи которых тригонометрические функции выражаются одна через другую.