
§ 9. Арккотангенс
Рассуждения, лежащие в основе определения и изучения свойств функции arc ctg х, аналогичны соответствующим рассуждениям, относящимся к арктангенсу. Поэтому мы ограничимся кратким конспективным изложением теории арккотангенса, предоставляя читателю в качестве упражнения самостоятельно провести надлежащие доказательства.
В каждом из интервалов (kπ, (k+1)π) котангенс убывает от ∞ до -∞, а потому возможен переход к обратной функции.
Определение. Функция, обратная функции y = ctg x в интервале (0, π), называется арккотангенсом:
x = arc ctg y.
Иначе говоря:
Символом arc ctg y обозначается дуга, заключенная в интервале (О, π), котангенс которой равен х.
Примеры:
- arc ctg 0 = π/2;
- arc ctg (-1) = 3π/4;
- arc ctg √3 = π/6.
Функция y = arc ctg x определена для всех действительных значений х и в интервале -∞<x<∞ убывает от π до 0.
График функции y = arc ctg x легко построить, построив график функции x = ctg y и выделив ту ветвь, для которой ординаты заключены в промежутке (0, π) (черт. 25).
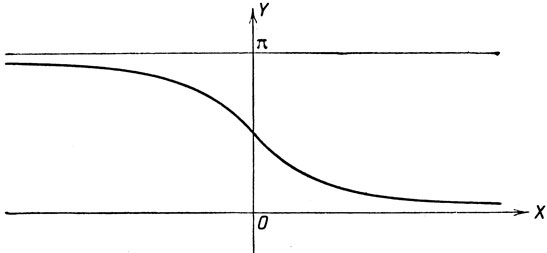
Черт. 25
При изменении знака аргумента арккотангенса имеем
arc ctg (-х) = π - arc ctg x.
Для интервала (kπ, (k+1)π) функция y = arc ctg x + kπ является обратной относительно котангенса.
В некоторых учебниках рекомендуется значение функции arc ctg х выбирать в промежутке (-π/2, π/2). Возможность выбирать значения arc ctg x в этом промежутке мотивируется тем, что в интервале (-π/2, π/2) котангенс может иметь любое заданное значение при одном единственном значении аргумента. Принять интервал (-π/2, π/2) за основной неудобно, так как он содержит точку разрыва котангенса. Если бы мы условились выбирать значение арккотангенса в этом интервале, то функция arc ctg x оказалась бы разрывной. График этой функции изображен на чертеже 26.
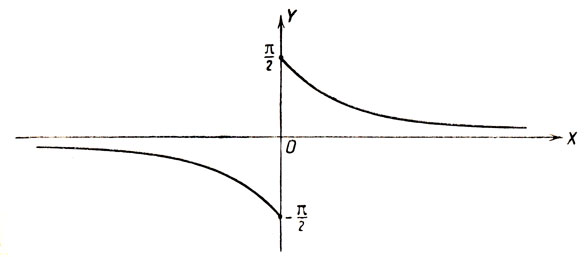
Черт. 26
Мы не будем останавливаться на рассмотрении практически редко встречающихся функций arc sec х и arc cosec x. Провести соответствующие рассуждения в качестве упражнения рекомендуем читателю. Ограничимся лишь следующим замечанием. Значения арксеканса и арккосеканса выбираются соответственно на сегментах
[0, π] и 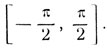
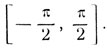
Функции arc sec х и arc cosec x определены для значений аргумента, не меньших единицы. Поэтому область определения этих функций распадается на две части: x≤-1 и х≥1.
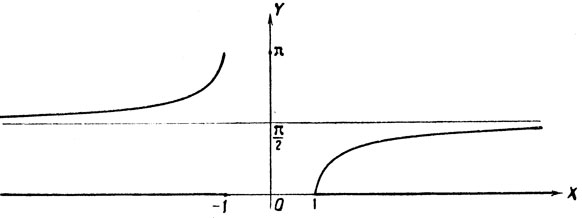
Черт. 27
На чертежах 27 и 28 изображены графики функций
arc sec х и arc cosec x.
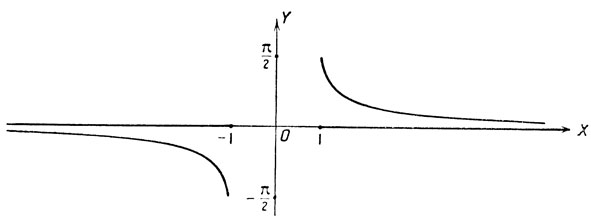
Черт. 28
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'