§ 8. Арктангенс

Точки x = ^π/₂ + kπ (k - любое целое число) разделяют всю числовую прямую на интервалы, в каждом из которых тангенс возрастает и может иметь любое заданное действительное значение, или, как говорят условно, в каждом из рассматриваемых интервалов тангенс возрастает от -∞ до ∞ (см. график черт. 14). Следовательно, в каждом из интервалов (-^π/₂ + kπ, ^π/₂ + kπ) возможен переход к обратной функции.

Определение. Функция, обратная функции y = tg x в интервале -^π/₂<x<^π/₂ называется арктангенсом:

В геометрической терминологии это определение формулируется так (меняем местами х и у): arc tg x есть дуга, взятая в интервале от -^π/₂ до ^π/₂:

тангенс которой равен х:

Итак, если y = arc tg x, то x = tg y, причем -^π/₂<y<^π/₂. Так как значение тангенса в интервале от -^π/₂ до ^π/₂ может быть произвольным действительным числом, то допустимыми значениями х являются произвольные действительные значения, и, следовательно, областью определения функции y = arc tg x является множество всех действительных чисел -∞<x<∞. Взаимно обратные функции y = arc tg x и x = tg y взаимно однозначно отображают друг на друга интервалы

(Черт. 22).

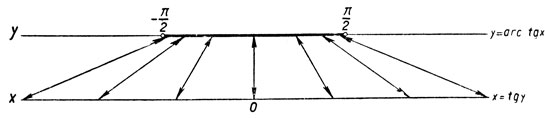
Черт. 22

Примеры:

1. arc tg 1 = ^π/₄;
2. arc tg √3 = ^π/₃;
3. arc tg (-1) = -^π/₄;
4. arc tg (-¹/_√3) = - ^π/₆;
5. 
6. 

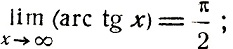
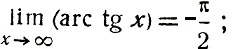
Отметим следующие основные свойства арктангенса.

1°. Функция y = arc tg х в интервале -∞<х<∞ возрастает от -^π/₂ до ^π/₂ (сами граничные значения ±^π/₂ исключаются). Это следует из монотонности и взаимной однозначности отображения друг на друга интервалов:

2°. При изменении знака аргумента имеет место равенство:

Доказательство аналогично доказательству соответствующего свойства арксинуса.

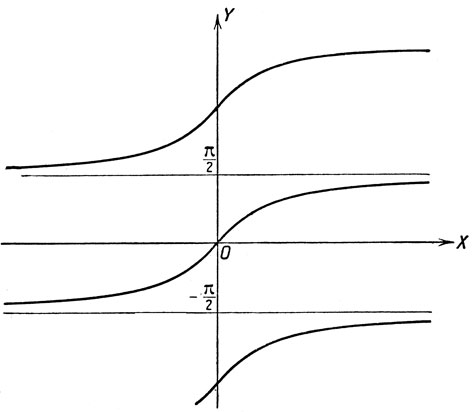
Черт. 23

Для построения графика функции y = arc tg x строим график функции x = tg y (черт. 23) и выделяем ветвь, для которой ординаты заключены в промежутке -^π/₂<y<^π/₂ (черт. 24).

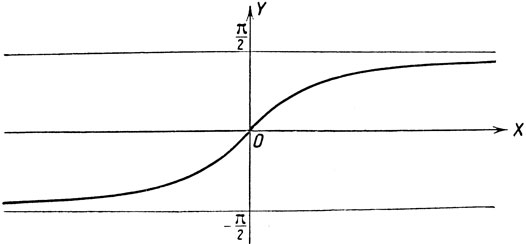
Черт. 24

В каждом из интервалов (-^π/₂+kπ, ^π/₂+kπ), получающихся сдвигом основного интервала (-^π/₂, ^π/₂) на любое целое число периодов тангенса (в силу монотонности) возможен переход к обратной функции. Если y = tg x, то обратной функцией в интервале -^π/₂+kπ<x<^π/₂+kπ будет

Примеры:

1. Найти дугу в интервале (-^3π/₂, -^π/₂), тангенс которой равен -√3. Имеем -^3π/₂ = -^π/₂ - π и -^π/₂ = ^π/₂ - π. Поэтому искомая дуга есть:
   arc tg(-√3) - π = - ^π/₃ - π = -^4π/₂.

Найти дугу в интервале (^π/₂, ^3π/₂), тангенс которой равен ^√3/₃, имеем ^π/₂ = -^π/₂ + π и ^3π/₂ = ^π/₂ + π. Искомая дуга есть