§ 7. Арккосинус

Если рассматривать функцию y = cos x при всевозможных действительных значениях х, то осуществить переход к обратной функции невозможно. На сегменте 0≤x≤π (т. е. I и II четверти) cos x убывает от 1 до -1, а потому существует обратная функция.

Определение. Функция, обратная функции y = cos x на сегменте 0≤х≤π, называется арккосинусом:

В геометрических терминах это определение формулируется так (меняем местами буквы х и у):

arc cos х есть дуга, взятая в промежутке от 0 до π:

косинус которой равен х:

где -1≤х≤1.

Областью определения функции arc cos x является сегмент [-1,1]. Если |x|>1, то arc cos x не имеет смысла.

Примеры:

1. arc cos 0 = ^π/₂;
2. arc cos 1 = 0;
3. arc cos (- 1) = π;
4. arc cos ¹/₂ = ^π/₃;
5. arc cos (-^1;/₂) = ^2π/₃;
6. arc cos ^√2/₂ = ^π/₄;
7. arc cos (-^√2/₂) = ^3π/₄;
8. arc cos (- 2) не имеет смысла.

Отметим следующие основные свойства арккосинуса:

1°. На сегменте -1≤х≤1 функция y = arc cos x убывает от π до нуля.

Это следует из того, что обратная функция x - cos y на сегменте 0≤y≤π убывает от 1 до -1.

2°. Имеет место равенство:

Доказательство. Дуга arc cos (-х) заключена на сегменте [0, π], в силу определения арккосинуса. Дуга π - arc cos x заключена в том же промежутке; это следует из неравенств 0≤ arc cos x≤π. Обе дуги имеют одинаковый косинус:

Отсюда следует равенство (1), ч. т. д.

Черт. 20

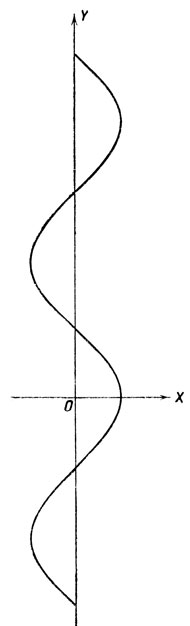
Построим график функции y = arc cos x. Согласно определению этой функции, имеем x = cos y. Графиком является косинусоида с волнами, расположенными вдоль оси ОY (черт. 20). Выделяя на этой линии дугу, для которой ординаты заключены в промежутке [0, π|, получим график функции arc cos х (черт. 21).

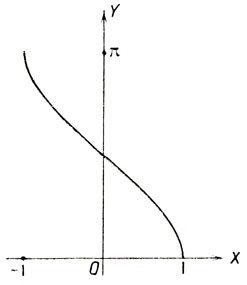
Черт. 21

Переход к обратной функции можно осуществить в любом промежутке, в котором косинус является монотонным. Так, y = cos х возрастает от - 1 до 1 на сегменте [-π, 0], соответствующая обратная функция есть - arc cos x. Вообще на сегменте [2kπ, (2k+1) π], на котором y = cos x убывает от 1 до -1, обратная функция есть

На сегменте [(2k-1)π; 2kπ], на котором y = cos х возрастает от -1 до 1, обратная функция есть

Примеры:

1. Найти дугу на сегменте [π; 0], косинус которой равен ¹/₂. Искомой дугой является
   - arc cos ¹/₂ = - ^π/₃.
2. На сегменте [π, 2π] найти дугу, косинус которой равен -¹/_√2. Имеем π = - π + 2π и 2π = 0 + 2π. Решение задачи дает дуга
   - arc cos (-¹/_√2) + 2π = - ^3π/₄ + 2π = ^5π/₄.