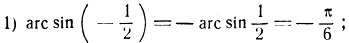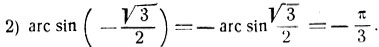Глава II. Обратные тригонометрические функции (аркфункции)
§ 6. Арксинус
Для тригонометрической функции y = sin x, рассматриваемой при всевозможных действительных значениях х, переход к обратной функции невозможен. Так, например, значение y = 0 функция имеет при бесконечно многих значениях аргумента x = kπ и по данному значению y не представляется возможным найти одно единственное значение х. Однако переход к обратной функции станет возможным, если рассматривать y = sin x не при произвольных значениях х, а лишь в каком-либо промежутке, в котором синус является монотонным.
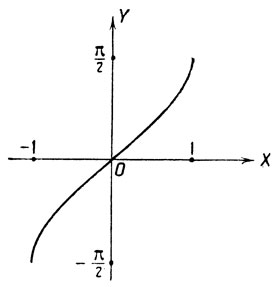
Рассмотрим сегмент -π/2≤x≤π/2. На этом сегменте sin x возрастает от -1 до 1 и, следовательно, значения x и y связаны взаимно-однозначным соответствием. Как показывает чертеж 16, сегменты -π/2≤x≤π/2 и -1≤y≤1 взаимно-однозначно отображаются друг на друга.
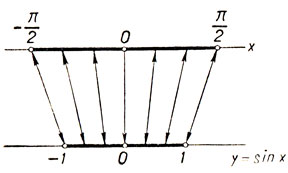
Черт. 16
Определение. Функция, обратная функции y = sin x, на сегменте -π/2≤x≤π/2, называется арксинусом и обозначается так:
x = arc sin y.
Теперь мы рассматриваем у как аргумент, а х как функцию. Чтобы не нарушать привычки в обозначениях (что не имеет принципиального значения), переставив буквы х и у, будем писать у = arc sin х, тогда имеем:
x = sin y,
где -π/2≤y≤π/2, а -1≤х≤1.
В геометрической терминологии определение арксинуса можно формулировать следующим образом: arc sin x есть дуга, взятая в пределах от -π/2 до π/2:
-π/2≤arc sin x ≤π/2,
синус которой равен числу х, где -1≤х≤1:
sin (arc sin х) = х.
Если |х|>1, то выражение arc sin х теряет смысл, так как не существует дуги, для которой значение синуса по абсолютной величине больше 1. Значит, областью определения функции arc sin х служит сегмент [-1, 1].
Таким образом (в силу определения), при любом значении |x|≤1 имеют место неравенства:
-π/2≤arc sin x≤π/2.
На основании этого же определения имеем:
sin (arc sin x) = x
(синус дуги, синус которой равен х).
Примеры.
- arc sin 1/2 = π/6;
- arc sin √3/2 = π/3;
- arc sin (-1/2) = - π/6;
- arc sin 1 = π/2;
- arc sin (-1) = - π/2;
- arc sin (-√/2) = -π/3;
- arc sin 0 = 0;
- arc sin 3 не имеет смысла.
Отметим следующие основные свойства арксинуса:
1°. Функция y = arc sin х на сегменте -1≤х≤1 возрастает от -π/2 до π/2.
Это следует из монотонности синуса и взаимной однозначности отображения друг на друга сегментов:
-1≤x≤1 и -π/2≤y≤π/2.
2°. При изменении знака аргумента функция arc sin x изменяет знак, не изменяя абсолютной величины:
arc sin (-х) = arc sin x. (1)
Доказательство. Дуга arc sin (-х) заключена на сегменте 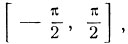 ибо значения арксинуса при любом аргументе заключены на этом сегменте. Дуга -arc sin x заключена на том же сегменте, в самом деле:
ибо значения арксинуса при любом аргументе заключены на этом сегменте. Дуга -arc sin x заключена на том же сегменте, в самом деле:
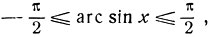
откуда
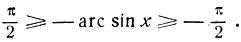
Обе дуги имеют одинаковый синус:
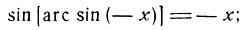
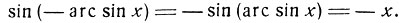
Отсюда вытекает равенство (1), ч. т. д.
Примеры:
Для построения графика функции y = arc sin x построим график функции x = sin y, при этом мы получим синусоиду с волнами, расположенными вдоль оси ОY (черт. 17). Выделяя на полученной линии дугу, для которой ординаты заключены на сегменте 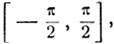 получим график арксинуса (черт. 18).
получим график арксинуса (черт. 18).
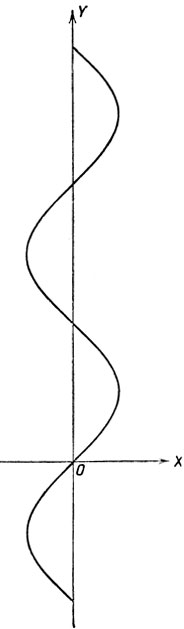
Черт. 17
Функция y = sin x имеет обратную функцию не только на сегменте 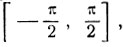 но и на любом сегменте, на котором она монотонна. Так, например, на сегменте
но и на любом сегменте, на котором она монотонна. Так, например, на сегменте 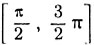 (т. е. во II и III четвертях) y = sinx убывает от 1 до -1, поэтому на данном сегменте возможен переход к обратной функции. Дугу x, имеющую синус, равный y, и расположенную на сегменте
(т. е. во II и III четвертях) y = sinx убывает от 1 до -1, поэтому на данном сегменте возможен переход к обратной функции. Дугу x, имеющую синус, равный y, и расположенную на сегменте 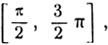 нетрудно найти. Для этого достаточно воспользоваться общей формулой приведения:
нетрудно найти. Для этого достаточно воспользоваться общей формулой приведения:
sin α = sin (π - α).
Черт. 18
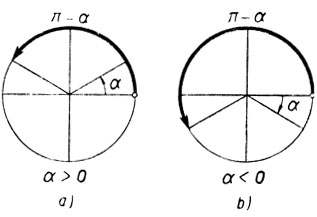
Если дуга α заключена на сегменте -π/2≤α≤π/2 (I отрицательная и I четверти), то дуга π-α заключена на сегменте 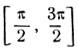 (II и III четверти):
(II и III четверти):
π/2≤π-α≤3π/2 (черт. 19.)
Черт. 19
Следовательно, х = π - arc sin x есть функция, обратная по отношению y = sin x на сегменте π/2≤x≤3π/2.
Функция y = sin x возрастает от -1 до 1 на сегменте -π/2+2kπ≤x≤π/2+2kπ (где k - любое целое число), функция
x = arc sin у + 2kπ
есть соответствующая обратная функция.
На сегменте π/2+2kπ≤х≤3π/2+2kπ функция у = sin x убывает от +1 до -1, а х = (π - arc sin y) + 2kπ есть соответствующая обратная функция.
Примеры.
1) На сегменте 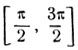 найти дугу γ, имеющую синус, равный 1/2. Согласно полученным результатам, эту дугу можно найти так:
найти дугу γ, имеющую синус, равный 1/2. Согласно полученным результатам, эту дугу можно найти так:
γ = π - arc sin 1/2 = π - π/6 = 5π/2.
Решим ту же задачу при следующих данных: синус искомой дуги равен - 1/√2:
γ = π - arc sin (-1/√2:) = π + π/4 = 5π/4
2) На сегменте 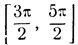 найти дугу, синус которой равен - 1/√2.
найти дугу, синус которой равен - 1/√2.
Так как
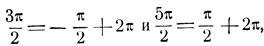
то искомой дугой является дуга
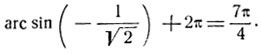
3) На сегменте 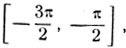 найти дугу, синус которой равен
найти дугу, синус которой равен 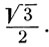 Так как
Так как
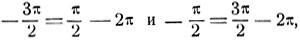
то искомой дугой будет дуга:
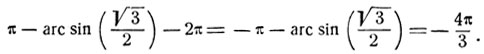
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'