§ 5. Тригонометрические функции и их основные свойства

Напомним те основные сведения из тригонометрии, которые необходимы для дальнейшего.

Тригонометрические функции рассматриваются первоначально как функции угла, так как численное значение каждой из них (если только оно имеет смысл) определяется заданием угла. Взаимно-однозначное соответствие между дугами окружности и центральными углами позволяет рассматривать тригонометрические функции как функции дуги. Так, например, аргумент функции sin φ мы имеем возможность по желанию толковать как угол или как дугу. Таким образом, первоначально аргумент тригонометрической функции выступает как геометрический объект - угол или дуга. Однако как в самой математике, так и в ее приложениях возникает потребность рассматривать тригонометрические функции как функции от числового аргумента. Даже в школьной математике не всегда аргумент тригонометрической функции рассматривается как угол. Так, например, гармоническое колебательное движение задается при помощи уравнения: s = A sin at. Здесь аргумент t есть время, а не угол (коэффициент а - число, характеризующее частоту колебания).

Процесс измерения углов (или дуг) ставит в соответствие всякому углу (дуге) в качестве его меры некоторое число. В результате измерения угла (дуги) может получиться любое действительное число, так как мы можем рассматривать направленные углы (дуги) любой величины. Выбрав определенную единицу измерения углов (дуг), можно всякому углу (дуге) поставить в соответствие измеряющее его число, и, обратно, всякому числу поставить в соответствие угол (дугу), измеряющийся данным числом. Это позволяет толковать аргумент тригонометрической функции как число. Рассмотрим какую-нибудь тригонометрическую функцию, например, синус. Пусть х - любое действительное число, этому числу соответствует вполне определенный угол (дуга), измеряющийся числом х, а полученному углу (дуге) соответствует вполне определенное значение синуса, sin x. В конечном итоге получается соответствие между числами: каждому действительному числу х соответствует вполне определенное действительное число y = sin x. Следовательно, sin x можно толковать как функцию числового аргумента. При рассмотрении тригонометрических функций как функций числового аргумента условились в качестве единицы измерения дуг и углов принимать радиан. В силу этого соглашения символы sin x, cos x, tgx и ctg x следует толковать как синус, косинус, тангенс и котангенс угла (дуги), радианная мера которого выражается числом х. Так, например, sin 2 есть синус дуги, измеряющейся двумя радианами^*.

^* (Заметим, что в некоторых руководствах радианная мера крайне неудачно называется отвлеченной, в отличие от градусной. Между обоими способами измерения нет принципиальной разницы, только лишь выбраны разные единицы измерения. К сожалению, и до сих пор этот вопрос иногда порождает псевдонаучное, вредное "методическое" пустословие.)

Выбор единицы измерения дуг и углов не имеет принципиального значения. Выбор радиана не диктуется необходимостью. Радиан оказывается лишь наиболее удобной единицей, так как в радианном измерении формулы математического анализа, относящиеся к тригонометрическим функциям, принимают наиболее простой вид^*.

^* (Это упрощение и объясняется тем, что в радианной мере 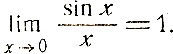Примем, например, за единицу измерения углов градус. Пусть t и х соответственно градусная и радианная меры данного угла, тогда имеем:

)

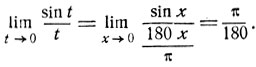
Закон соответствия между значениями аргумента и тригонометрической функции устанавливается не прямым указанием математических операций (формулой), которые надлежит выполнить над аргументом, а геометрически^*. Однако, чтобы иметь возможность говорить о функции, необходимо наличие закона соответствия, в силу которого каждому допустимому значению аргумента соответствует определенное значение функции, но не существенно, каким способом этот закон устанавливается.

^* (Средствами элементарной математики невозможно построить формулы, выражающие значения тригонометрических функций при помощи алгебраических действий над аргументом. Формулы, известные из высшей математики, выражающие значения тригонометрических функций непосредственно через значение аргумента,

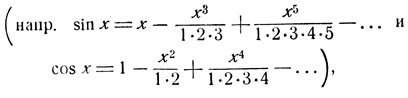
содержат, кроме алгебраических действий, операции предельного перехода (суммирование рядов, бесконечные произведения и пр.).)

Функции sin х и cos х имеют смысл при любых действительных значениях x, а потому областью их определения является множество всех действительных чисел.

Функция tg x определена для всех действительных значений x, отличных от чисел вида ^π/₂ + kπ.

Функция ctg x определена для всех действительных значений x, отличных от чисел вида kπ.

Итак, аргумент тригонометрической функции по нашему усмотрению можно толковать как угол, или как дугу, или, наконец, как число. Называя аргумент дугой (или углом), можно подразумевать под ним не саму дугу (или угол), а число, ее измеряющее. Сохраняя геометрическую терминологию, мы позволим себе вместо, например, такой фразы: "синус числа ^π/₂" говорить: "синус дуги ^π/₂".

Геометрическая терминология тем удобна, что она напоминает о соответствующих геометрических образах.

Одним из важнейших свойств тригонометрических функций является их периодичность. Функции sin x и cos x имеют период 2π. Это значит, что при любом значении х имеют место равенства:

где k - любое целое число.

Строго говоря, функции sin x и cos x имеют бесконечное множество периодов:

число 2тг, являющееся наименьшим положительным периодом, принято называть просто периодом.

Свойство периодичности имеет следующее геометрическое толкование: значение тригонометрических функций sin x и cos х не изменяется, если к дуге х прибавить (или вычесть) целое число окружностей. Если функция sin x или cos x обладает каким-либо свойством при значении аргумента х = а, то она обладает тем же свойством при любом из значений a + 2kπ.

Функции tg x и ctg x также являются периодическими, их периодом (наименьшим положительным) является число π.

При исследовании свойств периодической функции достаточно рассмотреть ее в каком-либо промежутке, по величине равном периоду.

Перечислим основные свойства тригонометрических функций.

1°. Функция sin х на сегменте 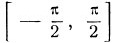(I и I отрицательная четверти) возрастает. Значения синуса в концах сегмента, т. е. при х = ^π/₂ и при х = - ^π/₂ равны соответственно 1 и -1.

2°. Каково бы ни было действительное число k, по абсолютной величине не большее 1, на сегменте - ^π/₂≤x≤^π/₂ существует единственная дуга х = х₁, синус которой равен k. Иначе говоря, на сегменте 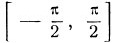синус имеет при одном единственном значении аргумента х = х₁ произвольное заданное значение, не превосходящее по абсолютной величине 1.

В самом деле, по данному значению синуса можно в I и I отрицательной четвертях тригонометрического круга (радиус тригонометрического круга всегда будем считать равным 1) построить соответствующую дугу. Достаточно отложить на вертикальном диаметре отрезок величиной k (вверх при k>0 и вниз при k<0) и провести параллель горизонтальному диаметру (черт. 10) до пересечения с правой полуокружностью. Найденная точка пересечения определит конец искомой дуги. Из геометрического построения следует, что (при |k|≤1) эта точка пересечения является единственной.

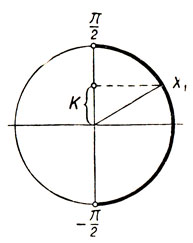
Черт. 10

Свойства 1° и 2° обычно объединяют в виде следующего условного утверждения.

На сегменте -^π/₂≤x≤^π/₂ синус возрастает от -1 до 1.

При помощи аналогичных геометрических рассуждений, или воспользовавшись формулой приведения sin (π - х) = sin x, нетрудно установить, что на сегменте ^π/₂≤x≤^3π/₂ (т. е. во II и III четвертях) синус убывает от 1 до -1. Сегменты -^π/₂≤x≤^π/₂ и ^π/₂≤x≤^3π/₂ вместе составляют полную окружность, т. е. охватывают полный период синуса. Дальнейшее исследование синуса становится излишним, и мы можем утверждать, что на любом сегменте [-^π/₂+2kπ, ^π/₂+2kπ] синус возрастает от -1 до 1, а на любом сегменте [^π/₂+2kπ, ^3π/₂ +2kπ] синус убывает от 1 до -1. График синуса представлен на чертеже 11.

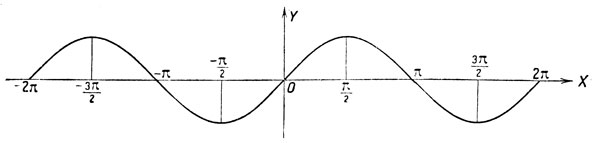
Черт. 11

Исследование косинуса проводится аналогично. Основные свойства косинуса таковы:

Функция cos x на сегменте [0, π] (т. е. в I и II четвертях) убывает от 1 до -1. На сегменте [π, 2π] (т. е. в III и IV четвертях) косинус возрастает от -1 до 1. В силу периодичности косинус убывает от 1 до -1 на сегментах [2π, (2k+1)π] и возрастает от -1 до 1 на сегментах [(2k-1)π, 2kπ] (черт. 12).

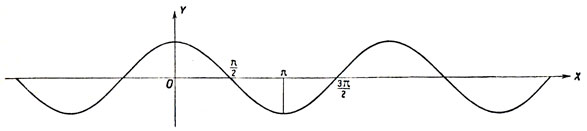
Черт. 12

Рассмотрим функцию y = tg x в интервале (-^π/₂, ^π/₂).

Граничные значения ±^π/₂ следует исключить, ибо tg (±^π/₂) не существует.

1 °. В интервале (-^π/₂, ^π/₂) функция tg х возрастает.

2°. Каково бы ни было действительное число k, в интервале - -^π/₂<x<^π/₂ у существует единственная дуга х₁, тангенс которой равен k.

В существовании и единственности дуги х₁ легко убедиться из геометрического построения, представленного на чертеже 13.

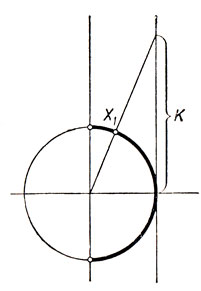
Черт. 13

Итак, в интервале (-^π/₂, ^π/₂) тангенс возрастает и при единственном значении аргумента имеет произвольное заданное действительное значение. Свойства 1° и 2° кратко формулируют в виде следующего утверждения:

в интервале (-^π/₂, ^π/₂) тангенс возрастает от -∞ до ∞.

Каково бы ни было заданное (как угодно большое) положительное число N, значения тангенса больше N при всех значениях x, меньших ^π/₂ и достаточно близких к ^π/₂. Символически это утверждение записывается так:

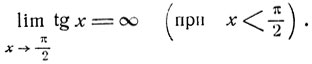
При значениях х, больших -^π/₂ и достаточно близких к -^π/₂ у значения tg x< -N. Это свойство символически записывается так:

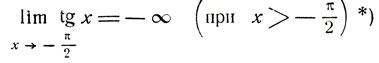
^* (Нередко пишут tg ^π/₂ = ∞ и говорят, что значение тангенса ^π/₂ равно ∞. Это утверждение в курсе элементарной математики может привести лишь к нелепым антинаучным представлениям. Символ ∞ не есть число и не может быть значением функции. Точный смысл, в котором следует употреблять символы ±∞, разъяснен в тексте.)

Дальнейшее исследование тангенса излишне, ибо величина интервала (-^π/₂, ^π/₂) равна π, т. е. полному периоду тангенса. Следовательно, в любом интервале (-^π/₂ + π, ^π/₂ + π) тангенс возрастает от -∞ до ∞, а в точках x = ^(2k+1)π/₂ имеет смысла. График тангенса представлен на чертеже 14.

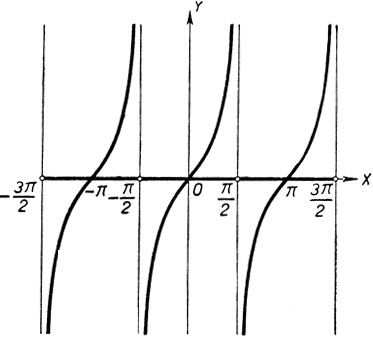
Черт. 14

Функция ctg x в интервале (0, π), а также в каждом из интервалов (kπ, (k+1)π) убывает от ∞ до -∞, а в точках х = kπ котангенс не имеет смысла. График котангенса представлен на чертеже 15.

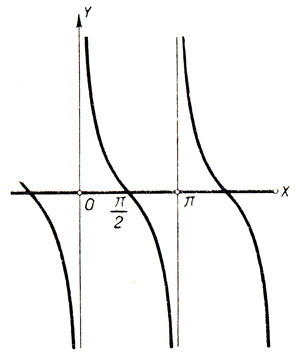
Черт. 15