§ 4. Обратная функция

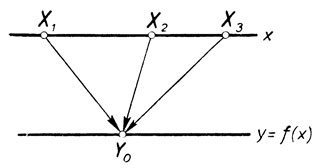
Пусть у = f(х) есть некоторая функция от аргумента x. Рассмотрим некоторое значение у₀ данной функции. Значение у₀ функция f(х) может иметь при нескольких (может быть, при бесконечно многих) значениях аргумента (черт. 4). Так, например, функция у = х² имеет значение y₀ = 4 при двух различных значениях: х₁ = 2 и х₂ = - 2. Функция у = sin х имеет значение у₀ = 0 для бесконечного множества значений аргумента:

Черт. 4

Функция

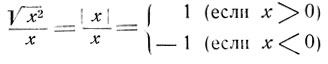
(черт. 5)^*

^* (Речь идет об арифметическом значении корня, в силу чего имеем √х² = |х|.)

Черт. 5

имеет значение, равное 1 для бесконечного множества значений аргумента, именно при всех положительных значениях x.

Всякому значению y функции y = f(x) можно поставить в соответствие все те значения x, при которых значение f(x) равно y. Однако такое обратное соответствие не всегда определяет x как функцию от у. В самом деле, данному численному значению y = y₀ может соответствовать не одно, а несколько значений x (черт. 6), а по определению функции каждому данному значению аргумента должно соответствовать одно единственное значение функции^*.

^* (Иногда вводится в рассмотрение понятие многозначной функции, когда каждому значению аргумента ставится в соответствие несколько (или бесконечное множество) значений функции. Однако мы не считаем целесообразным введение понятия многозначной функции в теорию функций от действительного аргумента.)

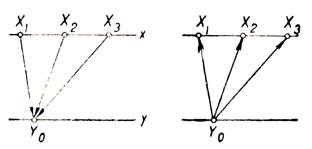
Черт. 6

Рассмотрим, например, функцию у = х², обратное соответствие каждому положительному значению у ставит в соответствие два различные значения х:

а потому не определяет х как функцию от y.

В частных случаях возможно, что обратное соответствие каждому допустимому значению у ставит в соответствие одно

единственное значение х, и тогда можно рассматривать х как функцию от аргумента у, эта функция называется обратной по отношению к данной. Переход к обратной функции возложен лишь в том случае, когда всякое данное значение функция имеет при одном единственном значении аргумента.

Примеры функций, имеющих обратную, знакомы из курса элементарной алгебры. Так, например, если y = x³, то

каждому действительному значению у соответствует единственное значение х, определяемое формулой

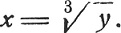
Если у = а^х (где а>0 и а≠1), то существует обратная функция x = lg_ay^*. Напротив, функция y = lg₂x, рассматриваемая на множестве всех действительных чисел -∞<х<∞, не имеет обратной функции.

^* (Существует убеждение, что для перехода к обратной функции необходимо из соотношения y = f(x) выразить х через y, а затем заменить х на y, а y на х. Так, например, если y = 2x, то x = lg₂y, а обратной функцией будет непременно y = lg₂x. Это убеждение основано на недоразумении. Функция определяется множеством значений аргумента и законом соответствия, а не буквами, которые употребляются для обозначения аргумента и функции. Так, например, выражения х², t², y² определяют одну и ту же, а не разные функции. Перестановка букв при переходе к обратной функции возможна и во многих случаях целесообразна, однако не обязательна.)

Если функция f(х) имеет обратную функцию, то значения y и х связаны взаимно-однозначным соответствием и могут быть объединены в пары взаимно-соответственных элементов (черт. 7).

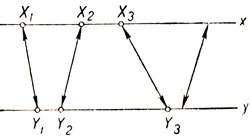
Черт. 7

Теорема. Всякая монотонная функция имеет обратную функцию.

Доказательство. Допустим для определенности, что функция y=f(x) возрастает, тогда большему значению аргумента, x₁<x₂, соответствует большее значение функции, y₁<y₂. Каждое данное (допустимое) значение y функция f(x) не может иметь при двух различных значениях аргумента х и х'. Так, например, если х<х', то f(x)<f(x') и не может выполняться равенство y = f(x) = f(x'). Следовательно, обратное соответствие является однозначным и определяет х как функцию от y, ч. т. д.

Для убывающей функции доказательство проводится аналогично.

Теорема. Если данная функция является возрастающей (убывающей), то обратная функция также является возрастающей (убывающей).

Доказательство. Предположим для определенности, что y = f(х) возрастает. Рассмотрим обратную функцию х = φ(у).

Пусть

покажем, что х₁<х₂ (черт. 8). В силу взаимной однозначности соответствия значений y и х имеем у = f(х). Неравенство у₁<y₂, или что то же f(x₁)<f(x₂), возможно в силу возрастания f(x) лишь при условии х₁<х₂, ч. т. д.

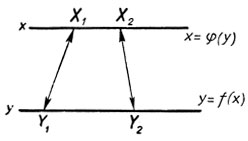
Черт. 8

Для убывающей функции (черт. 9) доказательство проводится аналогично.

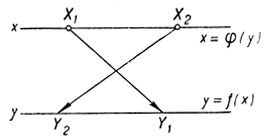
Черт. 9

Нередко, чтобы сделать возможным переход к обратной функции, рассматривают данную функцию не при всех допустимых значениях аргумента, а лишь в тех промежутках, в которых она монотонна. Рассмотрим, например, функцию у = х², считая допустимыми для х лишь неотрицательные значения. В промежутке 0≤x<∞ функция у = х² возрастает, каждому значению y соответствует единственное неотрицательное значение x, и мы получим обратную функцию:

Если функцию у = х² рассматривать при отрицательных значениях х, то также становится возможным переход к обратной функции: