§ 3. Монотонные функции

Определение. Функция y = f(x) называется возрастающей (убывающей) на данном промежутке, если при произвольных двух различных значениях аргумента, принадлежащих данному промежутку, большему значению аргумента соответствует большее (меньшее) значение функции:

для убывающей функции.

Функция возрастающая или убывающая в некотором промежутке называется монотонной в этом промежутке.

Примеры монотонных функций нетрудно привести из элементарной математики.

Примеры:

1. Функции x, x³, x⁵ - возрастающие.
2. Функции a^x, lg_ax возрастают при а>1 и убывают при а<1.
3. Функции ¹/_2^x, -x, -x³ убывающие.
4. Функции х², х⁴, x⁶, рассматриваемые в интервале -∞<x<∞, не являются монотонными. В самом деле, каждая из них убывает в промежутке -∞<x≤0 и возрастает в промежутке 0≤x<∞ (черт. 3).
   
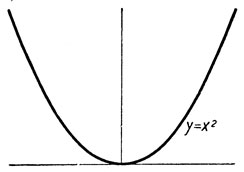
   Черт. 3