§ 2. Числовые промежутки

В дальнейшем мы будем встречаться главным образом с числовыми промежутками двух родов: с интервалами и с сегментами. Пусть а и b любые два действительные числа, взятые при условии а<b.

Определение.1°. Интервалом (а, b) называется множество всех действительных чисел x, удовлетворяющих неравенствам

2°. Сегментом [а, b] называется множество всех действительных чисел, удовлетворяющих неравенствам к

Геометрически интервал изображается на числовой прямой множеством точек, лежащих между двумя данными точками

Черт. 1

Черт. 2

а и b, при этом сами граничные точки a и bисключаются (черт. 1). Сегмент изображается на числовой прямой множеством точек, принадлежащих отрезку с концами в точках а и b, при этом сами концы а и bвключаются (черт. 2). Необходимость отличать сегмент от интервала возникает даже при изучении простейших элементарных функций. Так, например, областью определения функции √(1-х²) является сегмент [- 1,1]. Областью определения функции ¹/_√(1-х²) является интервал (-1,1), ибо теперь точки ±1 приходится исключить как обращающие в нуль знаменатель.

Функцию y = sin x можно рассматривать на сегменте 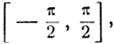однако функцию tg x нельзя рассматривать на этом сегменте, так как при х = ±^π/₂ тангенс теряет смысл.

Для записи утверждения, что под x можно подразумевать любое действительное число, принято писать символические неравенства -∞<x<∞. В целях установления единообразия в терминологии и в обозначениях, множество всех действительных чисел называется интервалом от -∞ до ∞ и обозначается так: (-∞, ∞). Аналогично запись а<x<∞ (или -∞<x<а) означает, что под x можно подразумевать любое число, большее (меньшее) a. Множество всех действительных чисел, больших (меньших) a, называется интервалом от a до ∞ (или от -∞ до a) и обозначается так: (a, ∞) или соответственно (-∞, a).