Глава I. Введение

§ 1. Понятие функции

Общее определение понятия функции формулируется следующим образом.

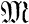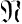Пусть и два множества, элементами которых могут быть любые объекты. Если каждому элементу х множества 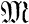ставится в соответствие некоторый элемент y множества 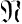, то говорят, что задана функция

Элементы х множества 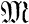называются значениями аргумента, а соответствующие элементы y множества 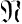- значениями функции. Множество 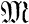называется областью определения функции, или множеством значений (допустимых) аргумента. Множество соответствующих значений y = f(х) называется множеством значений функции.

Таким образом, в основе понятия функции лежат понятия множества и соответствия. Эти понятия в современной математике являются первоначальными, не поддающимися определению через другие более простые понятия.

Примеры:

1. Процесс измерения отрезков (или углов) ставит в соответствие (по определенному правилу) всякому отрезку (углу) число - его меру. Следовательно, длина отрезка (мера угла) есть функция отрезка (угла). Здесь значения аргумента суть отрезки (углы), а значения функции - числа.
2. Аналогично, площадь многоугольника есть функция многоугольника. Здесь значения аргумента - многоугольники, а значения функции - числа.
3. При ортогональном проектировании на данную плоскость Р всякой точке х пространства ставится в соответствие точка y плоскости Р. Здесь значения аргумента суть точки пространства, а значения функции - точки плоскости.
4. В элементарной математике тригонометрические функции рассматриваются как функции угла (дуги). Так, например, всякому углу (дуге) соответствует значение синуса (число), здесь значения аргумента-дуги (углы), а значения функции - числа.

В дальнейшем мы будем рассматривать главным образом числовые действительные функции от действительного аргумента. Для этих функций множество 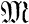- область определения - есть некоторое множество действительных чисел, значения функции суть действительные числа, а потому и множество значений функции есть также некоторое множество действительных чисел.

Закон соответствия данной функции может задаваться различными способами; так, например, он может быть задан непосредственным описанием или формулой, указывающей, какие математические операции следует выполнить над значением аргумента.

Примеры:

1. Поставим в соответствие всякому действительному числу х число у следующим образом: если х рациональное число, то считаем y = 1, если х - иррациональное число, то считаем у = 0. Эта функция задана непосредственным описанием закона соответствия.
2. Всякому действительному числу х поставим в соответствие число y, определяемое формулой
   y = 2^x + 1;
   здесь функция задается посредством математического выражения - формулы.
3. Всякому действительному числу х поставим в соответствие, число у следующим образом:
   
   
   Так, если х = 2, то у = 4; если х = 0, то y = 0, если х = - 5, то y = - 5. В последнем примере функция задается различными формулами в разных промежутках.

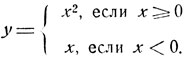
Пусть дано некоторое математическое выражение Т(х), содержащее букву х. Если заранее не указано, какие значения для х считаются допустимыми, то условимся допустимыми считать все те действительные значения х, при которых выражение T(x) имеет смысл и его значения действительны. Всякому допустимому значению x, соответствует вполне определенное значение выражения T(х), а потому рассматриваемое выражение определяет функцию от аргумента х. Областью определения этой функции является множество всех допустимых значений х.

Примеры:

1. у = ах² + bx + с область определения - множество всех действительных чисел.
2. y = √х область определения - множество неотрицательных чисел, х≥0.
3. y = √-x область определения - множество всех неположительных чисел, x≤.
4. y = ¹/_x²-1 область определения - множество всех действительных чисел, отличных от ± 1, т. е. х ≠ ± 1.
5. y = lg x область определения - множество всех положительных чисел, х>0.
6. y = lg sin x область определения состоит из промежутков, в которых синус положителен:
   2kπ<x<(2k+1)π (π - любое целое число).
7. y = √(-1-x²) выражение не определяет никакой (действительной) функции, так как ни при каком действительном x значение у не является действительным. Область определения есть "пустое множество".