21. Задача об ожерельях, функция Мёбиуса и синхронизируемые коды

Некоторые вопросы теории кодирования связаны с известной комбинаторной задачей, называемой "задачей об ожерельях". Эту задачу можно сформулировать следующим образом.

Пусть ожерелье состоит из бусинок нескольких цветов. Спрашивается, сколько существует различных ожерелий, если задано число бусинок каждого цвета.

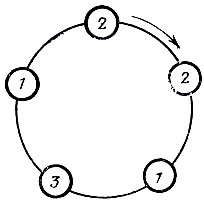
Расположим n бусинок по окружности, указав для каждой бусинки номер ее цвета. Если обойти эту окружность в определенном направлении, начав с некоторой бусинки, то ожерелью из n бусинок будет сопоставлено слово (a₁ а₂ ... а_n), где а_i есть номер цвета i-й бусинки. Но обход можно начать с любой бусинки, поэтому любому ожерелью соответствует n слов, получаемых одно из другого циклическими сдвигали. Например, для ожерелья, представленного на рисунке, получаем следующие слова:

Вообще говоря, среди n слов, сопоставленных ожерелью, могут быть и одинаковые. Нас, однако, будут интересовать не все ожерелья, а только такие, которые нельзя составить из двух или более одинаковых "кусков". Таким ожерельям отвечают слова, которые нельзя составить из нескольких одинаковых слов меньшей длины. Будем называть подобные слова основными. Например, слова 11, 100100100 не являются основными, а слово 1011 - основное. Ясно, что каждому "несоставному" ожерелью отвечает n различных основных слов.

Чтобы указать удобную формулу для числа основных слов, нам потребуется так называемая функция Мёбиуса ^*), определяемая следующим образом:

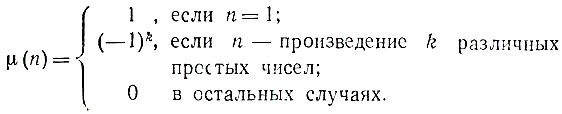
^*) (Август Фердинанд Мёбиус (1790-1868) - немецкий математик и астроном, известный, главным образом, своими работами по проективной геометрии. Им были впервые систематически изучены свойства функции μ(n).)

Обозначим через Р_n(m) общее число основных слов длины n алфавита из m символов. Тогда, как можно доказать,

где d₁, d₂, ..., d_k - все различные делители числа n. Формула (1) позволяет найти число интересующих нас ожерелий, которое, очевидно, равно Р_n(m)/n.

Выясним теперь, какое отношение имеет задача об ожерельях к проблемам кодирования. Дело в том, что при передаче закодированных сообщений должна соблюдаться определенная синхронность работы на передающей и приемной сторонах канала связи, которая обеспечивается дополнительными устройствами - тактовыми генераторами. При сбоях этих генераторов происходит нарушение синхронизации, и в качестве начального символа кодового слова воспринимается символ, который начальным не является. Отсюда актуальность задачи построения кодов, способных восстанавливать синхронизацию. Один из возможных путей ее решения (если отвлечься от исправления ошибок в символах) состоит в следующем. Будем рассматривать множество n-буквенных кодовых слов, удовлетворяющее такому ограничению: если (а₁ а₂ ... а_n) и (b₁ b₂ ... b_n) - кодовые слова (не обязательно различные), то никакое из "перекрытий" между ними

не является кодовым словом. Коды с этим свойством называют синхронизируемыми, и они, как легко понять, отвечают поставленной цели.

Как и обычно, платой за усовершенствование кода является уменьшение числа кодовых слов и, как обычно, возникает вопрос, насколько велика эта плата. Для ответа на этот вопрос как раз и можно использовать решение задачи об ожерельях. В самом деле, если а = (а₁ а₂ а₃ ... а_n) - кодовое слово синхронизируемого кода, то кодовым словом не может быть никакой его циклический сдвиг, так как он является перекрытием для пары (а, а). Кроме того, по той же причине всякое кодовое слово должно быть основным.

Поэтому максимальное число n-буквенных слов синхронизируемого кода, использующего алфавит из m символов, не превосходит числа несоставных ожерелий с n бусинками m различных цветов. Обозначив это число через W_n(m), имеем, следовательно,

Таким образом, пользуясь (1), получаем такую верхнюю границу для числа n-буквенных кодовых слов синхронизируемого кода:

(здесь d₁, ..., d_k по-прежнему все различные делители n). Можно доказать (но это достаточно сложно), что при нечетных n граница (2) действительно достигается, и что это, вообще говоря, не так, если n четно. Относительно простые выкладки показывают, что при больших n сумма в скобках близка к mⁿ, т. е. к общему числу слов длины n в m-буквенном алфавите, так что число допустимых слов синхронизируемого кода примерно в n раз меньше общего числа слов длины n.