
Задачи и дополнения
1. Доказать следующее свойство функции Мёбиуса: μ(nm) = μ(n)μ(m) для любых взаимно простых n и m.
2. Функция f называется сумматорной функцией для g, если
f(n) = ∑d\n g(d)
(запись d\n означает, что суммирование распространяется на все различные делители числа n).
Показать, что сумматорная функция для функции Мёбиуса равна нулю при n > 1 и единице при n = 1.
3. Пусть f - сумматорная функция для g (см. задачу 2). Верна следующая замечательная формула обращения Мёбиуса, лежащая в основе всех приложений функции μ(n):
g(n) = ∑d\n μ(n/d) f(d). (3)
Действительно,
∑d\n μ(n/d) f(d) = ∑d\n μ(n/d) ∑k\d g(k) = ∑d\n ∑k\d μ(n/d) g(k). (4)
В получившейся двойной сумме изменим порядок суммирования. Заметим для этого, что аргумент к функции g(k) при двойном суммировании пробегает всевозможные делители числа n, и если k фиксировано, то d пробегает все делители n, которые в свою очередь делятся на k. Поэтому двойную сумму (4) можно переписать в виде:
∑k\n ∑k\d\n g(k) μ(n/d) = ∑k\n g(k) ∑k\d\n μ(n/d), (5)
при этом запись k\d\n обозначает, что d пробегает все делители n, делящиеся на k. Введем обозначения m = n/d и t = n/k, тогда m пробегает всевозможные делители t и в силу утверждения задачи 2
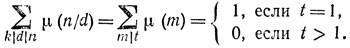
Следовательно,
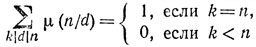
(k - делитель n).
Обращаясь теперь к выражению (5), мы видим, что в сумме по k
имеется лишь одно ненулевое слагаемое, отвечающее значению k = n, и потому
∑k\n g(k) ∑k\d\n μ(n/d) = g(n),
что равносильно (3).
4. Назовем число d периодом слова а, если а получается сочленением одинаковых слов длины d и не является сочленением одинаковых слов меньшей длины. Пусть Рd(m) означает общее число слов длины n в алфавите из m символов, имеющих период d.
Убедиться, что
∑d\n Pd(m) = mn,
и, пользуясь формулой обращения (3), получить оценку (2).
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'