17. Голосование

Хотя в процедуре принятия решения большинством голосов нет для нас ничего необычного, может все же показаться неожиданным, что метод голосования используется при декодировании помехоустойчивых кодов. Отчасти мы уже коснулись этого вопроса в § 8, когда рассказывали о коде с повторением, - решение о посланном символе принималось там как раз большинством голосов. Теперь же мы покажем, как применяется голосование в случае произвольного линейного кода.

Обратимся сначала к примеру. Здесь нам поможет неоднократно упоминавшийся ранее (7,3)-код, получающийся из (7,4)-кода Хемминга добавлением общей проверки на четность. Его проверочная матрица имеет вид:

Удобнее, однако, рассмотреть эквивалентный циклический код с порождающим многочленом g(x) = (x + 1) (x³ + x + 1) и с проверочной матрицей

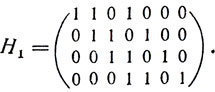
Эта матрица получена способом, указанным в дополнении 9 к § 11. В том, что коды с проверочными матрицами H и H₁ действительно эквивалентны, читатель может убедиться самостоятельно.

Пусть принято некоторое слово α₀ α₁ α₂ α₃ α₄ α₅ α₆, содержащее, быть может, ошибочные символы. Для каждого символа а; будем в отдельности решать, верен он или нет, используя те соотношения, которыми этот символ связан с остальными. Начнем с символа α₀ и выпишем некоторые содержащие его проверки. Первой строке матрицы H₁ отвечает проверочное соотношение α₀ + α₁ + α₃ = 0, сумме первой, второй и третьей строк - соотношение α₀ + α₄ + α₅ = 0, а сумме первой, второй и четвертой строк - соотношение α₀ + α₂ + α₆ = 0. Итак, имеем:

Если ошибки при передаче отсутствовали, то в принятом слове будет выполняться каждое из соотношений (1), а правые их части дадут верное значение для α₀. Соотношения (1) для символа α₀ выбраны с таким расчетом, что всякий другой символ входит в правую часть ровно одной проверки. Поэтому если лишь один из них ошибочен, то только в одном из соотношений (1) будет нарушено равенство. Учитывая это, можно предложить следующее правило для определения верного значения символа α₀: если среди значений α₁ + α₃, α₄ + α₅, α₂ + α₆, α₀ большинство составляют нули, то полагаем, что нуль и есть верное значение для α₀, если же большинство из них - единицы, то верным значением для α₀ считаем единицу. Такое голосование гарантирует верное решение, если принятое слово содержит не более одной ошибки. Возможно и равенство голосов (например, в случае двойной ошибки), и в этом случае приходится довольствоваться ее обнаружением.

Аналогичные проверки могут быть составлены и для других символов. Например, для α₁ имеем соотношения:

также обладающие тем свойством, что каждый символ входит в правую часть не более одного раза. Эти проверки получаются из системы (1) циклическим сдвигом на одну позицию. Последующие циклические сдвиги дают системы подобных проверок для остальных символов.

Анализируя указанным способом каждый символ принятого слова, мы правильно восстановим посланное кодовое слово, если произошло не более одной ошибки, и обнаружим любую двойную ошибку. Тем самым полностью используются корректирующие способности данного кода - ведь его кодовое расстояние равно 4.

Разобранный нами метод исправления и обнаружения ошибок называют мажоритарным декодированием (т. е. декодированием по принципу большинства). Применим он тогда, когда - как в нашем примере - для каждого символа α_j существует система проверок

обладающая тем свойством, что в правую часть каждой проверки входят символы, отличные от α_j, и всякий такой символ входит не более чем в одну проверку. Такая система проверок называется ортогональной (или разделенной). Если число проверок, входящих в каждую ортогональную систему, не меньше s, то путем голосования могут быть исправлены любые t ошибок, где t < (s + l) / 2. В самом деле, ошибка в одном символе влияет в силу ортогональности не более чем на одну проверку, следовательно, среди значений символа α_j, которые даются всеми соотношениями (2), неправильными могут оказаться не более t, т. е. не более половины значений. Тогда, сравнивая значения правых частей проверок, а также значение самого символа α_j, мы по большинству голосов определяем верное значение этого символа. Если же (при нечетном s) t = (s + l) / 2, то имеет место равенство голосов, ошибка при этом хотя и обнаруживается, но не исправляется.

Случай, когда число s проверок в каждой ортогональной системе на единицу меньше кодового расстояния d, т. е. когда s = d - 1, является в известном смысле идеальным. В этом случае голосование позволяет, как и в рассмотренном примере, полностью реализовать корректирующие свойства кода. Код, для каждого символа которого существует система из (d - 1) ортогональных проверок, называется полностью ортогонализуемым.

Чем хорош метод голосования? Прежде всего тем, что его техническая реализация предельно проста (особенно в случае двоичных циклических кодов). Наряду с обычными сумматорами и ячейками памяти схема декодирования должна содержать мажоритарный элемент (логическую схему, осуществляющую выбор значения α_j по большинству голосов).

Вот как устроена принципиальная схема мажоритарного декодирования для (7,3)-кода, упомянутого выше (рис. 24, а).

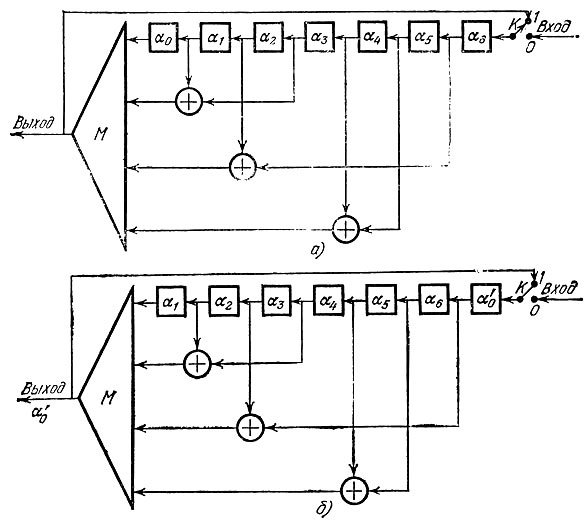
Рис. 24

В этой схеме М - мажоритарный элемент, осуществляющий голосование, K - переключатель, находящийся в положении 0 во время приема сообщения и в положении 1 при его декодировании. Рис. 24, а соответствует моменту, когда сообщение полностью поступило в запоминающий регистр и ключ K переводится в положение 1. Начинается декодирование. На первом его шаге (первый такт) на вход мажоритарного элемента подаются значения α₀, α₁ + α₃, α₂ + α₆, α₄ + α₅. На выходе его появляется символ α'₀, являющийся итогом голосования. В следующем такте происходит сдвиг сообщения в регистре, а символ α'₀ поступает в последнюю ячейку памяти. Этому моменту соответствует рис. 24, б.

Теперь уже голосование осуществляется по значениям α₁, α₂ + α₄, α₃ + α'₀, α₅ + α₆, и в результате получается значение α'₁ следующего символа сообщения. Дальнейшие такты работы схемы совершенно аналогичны. Если произошло не более одной ошибки, то последовательность (α₀, α₁, ..., α'₆) и есть верное кодовое слово.

Как мы видим, в схеме используется только информация о принятом слове; никакой дополнительной информации не требуется. А это очень важно, потому что именно необходимость хранения большого объема данных служит основным препятствием для применения некоторых методов декодирования (например, синдромного декодирования).

Еще одно немаловажное достоинство голосования по сравнению с другими методами декодирования заключается в том, что этот метод зачастую позволяет исправлять или обнаруживать многие ошибки, кратность которых превышает (d - 1) / 2.