Задачи и дополнения

1. Построить кодеры для двоичных циклических кодов чины 15 с порождающими многочленами

2. Всякий циклический (n, k)-код с порождающим многочленом g(х) можно представить в систематической форме следующим образом. Пусть r_i(х) - остаток от деления xⁱ на порождающий многочлен g(x), т. е.

Рассмотрим многочлены

при i = m, m+1, ..., n-1, где m = n-k - степень порождающего многочлена g(x). Все эти многочлены кодовые, так как они кратны g(x). Кодовый вектор, соответствующий многочлену xⁱ - r_i(x), имеет вид:

r_i0, r_i1, r_{i, m-1} - коэффициенты остатка r_i(x), а символ 1 стоит в позиции с номером i.

Мы получили n - m = k векторов, которые, как нетрудно видеть, линейно независимы. Если составить матрицу G, строками которой являются указанные векторы, то она и будет порождающей (ее строки образуют базис кодового подпространства). Если через R обозначить матрицу, строками которой являются коэффициенты многочленов r_i(x), то матрица G получается приписыванием к матрице - R справа единичной матрицы Е_k порядка k и ее можно условно записать в виде:

Отсюда легко следует (ср. § 11, задача 10), что в качестве проверочной можно взять матрицу

По столбцам матрицы Н стоят коэффициенты остатков от деления многочленов x⁰, х¹, ..., х^n-1 на g(x).

3. Чтобы проиллюстрировать метод, изложенный в дополнении 2, рассмотрим снова (7,4)-код с порождающим многочленом 1 + x² + x³. Имеем:

Строками порождающей матрицы являются, следовательно, коэффициенты многочленов:

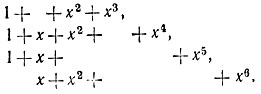
Таким образом,

и

4. Метод, рассмотренный в дополнении 2, можно использовать для построения кодера систематического циклического кода.

При кодировании с помощью матрицы (4) кодовое слово получается умножением информационного слова на эту матрицу (см. (6), § 11). В этом случае последние k символов а_m, а_m+1, ..., a_n-1 кодового слова совпадают с информационными символами, а все кодовое слово является линейной комбинацией строк порождающей матрицы (4) с коэффициентами а_m, а_m+1, ..., a_n-1. Учитывая, что по строкам матрицы R стоят коэффициенты остатков от деления многочленов хⁱ на порождающий многочлен g(x), мы убеждаемся, что величины а₀, а₁, ..., a_m-1 являются коэффициентами остатка от деления многочлена

на многочлен g(x) (в случае двоичных многочленов знак минус перед скобкой можно опустить).

Следовательно, схемы деления могут быть использованы для нахождения проверочных символов кодовых слов циклического кода в систематической форме и, в конечном итоге, для построения его кодера. На рис. 23 приведена схема кодера двоичного (7, 4)-кода с порождающим многочленом 1 + х² + х³, основанная на указанном принципе.

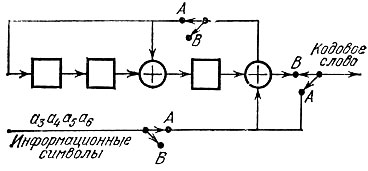
Рис. 23

Проследим вкратце работу этой схемы в течение семи тактов. Первые четыре такта переключатели схемы находятся в положении А, следующие три - в положении В. В первые четыре такта информационные символы поступают (без изменений) на выход всей схемы и на выход схемы деления. В течение этих четырех тактов в последовательных ячейках схемы деления получаются коэффициенты остатка а₀, а₁, а₂ от деления многочлена а₆x⁶ + а₅x⁵ + а₄x⁴ + а₃x³ на порождающий многочлен 1 + x² + x³, т. е. проверочные символы (в схеме на рис. 18 на это ушло бы семь тактов, но в данной схеме три такта "экономятся", так как последовательность коэффициентов а₆, а₅, а₄, а₃ подается не на вход, а сразу на выход схемы деления). В последующие три такта проверочные символы - сначала а₂, затем а₁, затем а₀ - поступают из схемы деления на выход всей схемы. Таким образом, по истечении семи тактов на выходе всей схемы получаем целиком кодовое слово.

Рекомендуем читателю проследить по тактам работу рассматриваемой схемы для случая а₃ = 0, a₄ = a₅ = a₆ = 1.