5. Еще о свойстве префикса и однозначной декодируемости

Возникает вопрос: каковы возможные длины кодовых слов однозначно декодируемого, в частности, префиксного кода? Понятно, например, что не существует двоичного префиксного кода с длинами кодовых слов 1, 1, 2. Несколько труднее ответить на такой вопрос: существует ли префиксный двоичный код, содержащий 100 слов с длинами от 1 до 100? Оказывается, существует. Кодовое дерево для требуемого кода, содержащее 100 "этажей", изображено на рис. 9 (пунктиром отмечены пропущенные этажи).

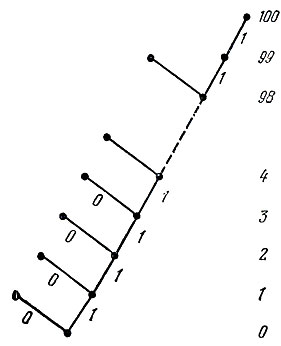
Рис. 9

Вопросы такого рода можно было бы продолжить, отвечая на них в каждом конкретном случае. Но на самом деле можно установить общие условия (необходимые и достаточные) для существования префиксного и вообще произвольного однозначно декодируемого кода.

Пусть V = {а₁, а₂, ..., a_N} - префиксный двоичный код, дерево которого схематически изображено на рис. 10.

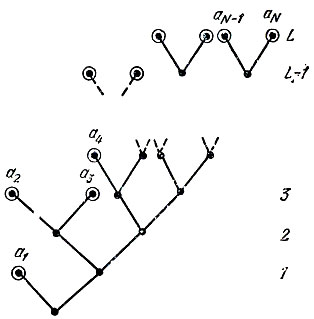
Рис. 10

Пусть n_k - число кодовых слов длины k (n_k совпадает с числом концевых вершин k-го этажа). Конечно, справедливо неравенство

так как 2^k - максимально возможное число вершин на k-м этаже двоичного дерева. Однако в случае префиксного кода для n_k можно получить гораздо более точную оценку, чем (1). В самом деле, если n₁, n₂, ..., n_k-1 - число концевых вершин 1; 2; ...; k-1 этажей дерева, то число всех вершин k-го этажа кодового дерева равно

и потому

или иначе

Деля обе части последнего неравенства на 2^k, получаем:

Неравенство (3) верно для любого k ≤ L (L - максимальная длина кодовых слов), в частности

Если l₁, l₂, ..., l_N - длины кодовых слов a₁, а₂, ..., a_N, то неравенство (4) запишется в таком виде:

Это и есть то условие, которому обязаны удовлетворять длины кодовых слов двоичного префиксного кода.

Оказывается, что неравенство (5), называемое в теории кодирования неравенством Крафта, является также достаточным условием того, чтобы существовал префиксный код с длинами кодовых слов l₁, l₂, ..., l_N.

Рассуждаем так. Если среди чисел l₁, l₂, ..., l_N имеется ровно n_i чисел, равных i, то неравенство (5) можно переписать в виде (4), где L - максимальное из данных чисел. Из справедливости (4) подавно следует, что верны неравенства (3) для всех k ≤ L, а, следовательно, и неравенство (2).

Обратимся к рис. 11, на котором изображено дерево "высоты" L, имеющее наибольшее число вершин и ветвей (ребер). Все концевые вершины (их 2^L) такого дерева находятся на последнем L-ом этаже, а из каждой вершины промежуточного этажа исходят ровно две ветви.

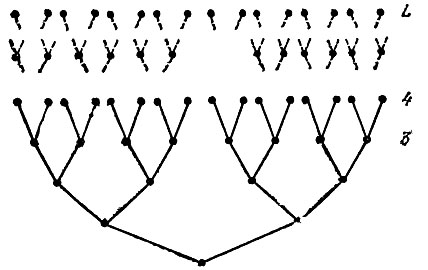
Рис. 11

Для построения нужного префиксного кода мы должны подходящим образом выбрать n₁ слов длины 1, n₂ слов длины 2, вообще n_k слов длины k (l ≤ k ≤ L) или, иными словами, n₁ концевых вершин на первом, n₂ - на втором, ..., n_k - на k-ом этаже.

Из неравенства (2) при k = l получаем n₁ ≤ 2, т. е. требуемое число не превосходит общего числа вершин первого этажа. Значит, на этом этаже можно выбрать какие-то n₁ вершин в качестве концевых (n₁ равно 0, 1 или 2). Если это сделано, то из общего числа вершин второго этажа (их 2² = 4) для построения кода можно использовать лишь 4-2n₁ (почему?). Однако нам хватит и этого числа вершин, так как из неравенства (2) при k = 2 вытекает

Аналогично, при k = 3 имеем неравенство:

Правая часть его вновь совпадает с допустимым для построения префиксного кода числом вершин третьего этажа, если на первых двух этажах уже выбраны n₁ и n₂ концевых вершин. Значит, снова можно выбрать n₃ концевых вершин на третьем этаже. Продолжая этот процесс вплоть до k = L, мы и получим требуемый код.

Если кодовый алфавит содержит d символов, то подобным же образом доказывается, что необходимым и достаточным условием для существования префиксного кода с длинами слов l₁, l₂, ..., l_N является выполнение неравенства

Оказывается, неравенству (6) обязаны удовлетворять и длины кодовых слов произвольного однозначно декодируемого кода. Поэтому, если существует однозначно декодируемый код с длинами слов l₁, l₂, ..., l_N, то существует и префиксный код с теми же длинами слов. Префиксными же кодами пользоваться удобнее по причине, указанной в дополнении 11 к § 4.