
Задачи и дополнения
1. Каково минимальное число слов полного двоичного префиксного кода с максимальной длиной L? Какими будут длины кодовых слов такого минимального кода? (Ответы на эти вопросы подсказывает рис. 9.)
Решить те же вопросы в случае d-ичного кода.
2. Доказать, что префиксный код является полным тогда и только тогда, когда в неравенстве Крафта достигается равенство:
d-l1 + d-l2 + d-lN = 1.
Указание. То, что из предыдущего равенства вытекает полнота, очевидно. Для доказательства обратного утверждения следует предположить, что неравенство (6) строгое, Тогда из него выводится строгое же неравенство
nL < dL - dL-1n1 - dL-2n2 - dnL-1,
которое показывает (почему?), что можно добавить по крайней мере еще одно слово, не нарушая префиксности.
3. Утверждение предыдущей задачи допускает следующую забавную интерпретацию, являющуюся одновременно и его доказательством (она заимствована из книги [6]).
Рассмотрим дерево, соответствующее полному префиксному коду. Представим себе, что на это дерево взбирается обезьяна. Начав с корня, она наугад выбирает любую из d исходящих из него ветвей; вероятность такого выбора равна 1/d. Добравшись до очередной развилки, обезьяна снова наугад выбирает некоторую ветвь с вероятностью 1/d (напомним, что из каждой промежуточной вершины дерева полного кода исходит ровно d ветвей). Тогда вероятность того, что обезьяна достигнет какой-то определенной концевой вершины, находящейся на высоте k, равна (1/d)k. Если таких вершин nk, то с вероятностью nkd-k обезьяна остановится на высоте k. На какой-то высоте от 1 до L обезьяне придется остановиться (вероятность этого равна 1). Поэтому
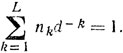
(В приведенном рассуждении мы использовали правила сложения и умножения вероятностей.)
4. Префиксный код с данными длинами кодовых слов может быть построен далеко не единственным способом. Пусть d-ичный префиксный код (не обязательно полный) имеет nk слов длины k (1 ≤ k ≤ L). Доказать, что число различных таких кодов с фиксированными L и nk равно произведению
(dn1) × (d2 - dn1n2) × (d3 - d2n1 - dn2n3) d2 ... × (dL - dL-1n1 - ... - dnL-1nL),
где (ij) = Cji - число сочетаний из i элементов по j.
Например, число двоичных префиксных кодов с L = 4, n1 = 0, n2 = 1, n3 = 2, n4 = 4 равно
C02 C14 C26 C48 = 4200.
5. Выше было доказано, что если для чисел l1, l2, ..., lN выполняется неравенство Крафта, то существует префиксный код с длинами l1, l2, ..., lN. Найти этот код можно, строя этаж за этажом его кодовое дерево. Другой более удобный метод решения этой задачи был придуман Шенноном, и (применительно к двоичным кодам) он состоит в следующем.
Пусть числа l1, l2, ..., lN удовлетворяют неравенству
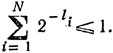
Можно считать, что l1 ≤ l2 ≤ ... ≤ lN. Рассмотрим последовательность чисел
q1 = 0; q2 = 2-l1; ...;
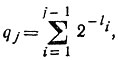
..., qN = ∑N-1i=1 2-li. (7)
Заметим, что все эти числа заключены в пределах 0 ≤ q < 1, поэтому каждое из них может быть представлено двоичной дробью вида ∑nk=1 αk2-k, где каждое αk есть 0 или 1. При этом из (7) можно заключить, что все эти дроби конечны, и двоичная запись для qj имеет не более lj значащих цифр. Таким образом, любое число qj однозначно представимо в виде:
qj = ∑lji=1 cij2-i,
где всякое cij есть 0 или 1. Следовательно, каждому qj однозначно отвечает слово υj = c1jc2j ... cljj длины lj. Рассмотрим код V = {υ1, υ2 ..., υN}. Покажем, что он обладает свойством префикса. Пусть υj и υk два слова (k > j). Тогда, согласно (7), qk - q≥j 2-lj, а это означает, что lj-й символ слова υj не совпадает с lj-м символом слова υk. Следовательно, υj не является началом υk, откуда и вытекает префиксность кода V.
Разъясним сказанное на примере. Построим префиксный код с длинами слов l1 = 1, l2 = l3 = 3, l4 = 4. В этом случае
q1 = 0; q2 = 1/2; q3 = 5/8; q4 = 3/4.
Двоичная запись этих чисел с нужным числом lj знаков следующая:
q1 = 0; q2 = 1/2 + 0/22 + 0/23; q3 = 1/2 + 0/22 + 1/23; q4 = 1/2 + 1/22 + 0/23 + 0/24.
В результате мы получим искомый код:
υ1 = 0; υ2 = 100; υ3 = 101; υ4 = 1100.
6. Используя метод Шеннона, найти префиксные коды с указанными ниже длинами слов:
а) l1 = l2 = 2; l3 = l4 = 3; l5 = l6 = l7 =4;
б) l1 = 1; l2 = 2; l3 = l4 = l5 = l6 = 4.
Построить кодовые деревья для полученных кодов. Определить, какой из этих кодов является полным.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'