
Задачи и дополнения
1. Префиксный код называют полным, если добавление к нему любого нового кодового слова (в данном алфавите) нарушает свойство префиксности. Убедиться, что двоичные коды, деревья которых изображены на рис. 3, 4, являются полными.
На рис. 7 представлено кодовое дерево префиксного, но неполного двоичного кода. Действительно, добавив к кодовым словам 0, 10, 111 слово 110, получим снова префиксный код.
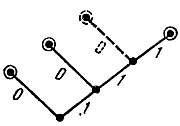
Рис. 7
2. Доказать, что двоичный код Фано является полным кодом. Верно ли аналогичное утверждение для кода Фано с произвольным основанием?
3. Проанализировав задачи 1 и 2, сформулировать необходимое и достаточное условие, которому должно удовлетворять кодовое дерево полного префиксного кода, и доказать его необходимость и достаточность.
4. Используя кодовое дерево, доказать, что всякий префиксный код может быть расширен до полного кода добавлением к нему некоторого множества кодовых слов.
5. Пусть k - максимальное значение длин кодовых слов префиксного кода. Показать, что число кодовых слов не превосходит величины 2k в случае двоичного кода и величины dk в случае кода с произвольным основанием d. При каких условиях достигается равенство?
6. Код, представленный на рис. 7, можно сделать более экономным, отбрасывая в слове 111 последний символ. При этом свойство префиксности не нарушится. Подобная операция, состоящая в том, что каждое слово префиксного кода заменяется наименьшим его началом, не являющимся началом других кодовых слов, называется усечением. Очевидно, что в результате усечения получается префиксный код и при этом более экономный, чем исходный. Возникают такие два вопроса:
1. Возможно ли усечение полного кода?
2. Можно ли утверждать, что в результате усечения получается полный код?
7. На рис. 8, а представлено кодовое дерево префиксного кода, для которого усечение невозможно. В то же время мы получим более экономный префиксный код (рис. 8, б), если в словах 110 и 111 вычеркнем второй символ 1.
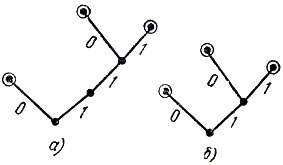
Рис. 8
Справедливо следующее утверждение: префиксный код является полным тогда и только тогда, когда его невозможно сократить (т. е. вычеркнуть хотя бы один знак в любом из кодовых слов), не нарушив свойства префикса.
8. Любопытно рассмотреть примеры однозначно декодируемых кодов, не обладающих свойством префикса. Пожалуй, простейшим примером такого рода является двоичный код {1, 10}. Ясно, что в любой кодовой последовательности, составленной из этих слов, всякое появление символа 1 означает начало нового кодового слова. Последнее остается справедливым для кода, каждое слово которого есть единица с последующими нулями. Разумеется, подобные коды далеко не самые экономные.
Приведем менее тривиальный пример однозначно декодируемого кода: {01, 10, 011}. Рекомендуем читателю указать алгоритм однозначного выделения кодовых слов из кодовой последовательности для этого кода.
9. Как узнать, является ли произвольный код однозначно декодируемым? Для этого можно предложить следующий способ. Возьмем всевозможные пары кодовых слов, в которых одно слово является префиксом другого. Для каждой такой пары найдем "повисший" суффикс, который остается после удаления префиксного слова из начальной части более длинного слова. Например, повисший суффикс для пары 10 и 10010 есть 010. Выпишем все повисшие суффиксы. Далее проделаем то же самое для каждой пары слов, состоящей из повисшего суффикса и кодового слова, в которой одно слово является префиксом другого. Выпишем все новые повисшие суффиксы, которые при этом получатся. Будем продолжать этот процесс до тех пор, пока будут появляться новые суффиксы. Код является однозначно декодируемым тогда и только тогда, когда никакой суффикс не совпадет ни с одним кодовым словом.
10. Выяснить, обладают ли свойством однозначной декодируемости следующие коды:
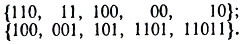
11. Префиксные коды иногда называют мгновенными (или мгновенно декодируемыми), поскольку конец кодового слова опознается сразу, как только мы достигаем конечного символа слова при чтении кодовой последовательности. В этом состоит преимущество префиксных кодов перед другими однозначно декодируемыми кодами, для которых конец каждого кодового слова, как мы видели, может быть найден лишь после анализа одного или нескольких последующих символов, а иногда и всей кодовой последовательности. Таким образом, в отличие от префиксного кода декодирование здесь осуществляется с запаздыванием по отношению к передаче сообщения.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'