4. Свойство префикса, или куда идти роботу

При использовании неравномерных кодов приходится сталкиваться с одной проблемой, которую мы поясним на примере кодовой таблицы 9 предыдущего параграфа. На первый взгляд разумно было бы укоротить второе и третье кодовые слова, отбросив в них последний символ, так как при этом основное наше требование сохраняется: по-прежнему различные сообщения кодируются разными словами, как это видно из получившейся новой кодовой таблицы.

Таблица 11

Но пусть, к примеру, данные сообщения - это команды) выдаваемые электронному роботу: А₁ - идти прямо, А₂ - повернуть назад, А₃ - свернуть влево, А₄ - свернуть вправо. Предположим, что программа поведения робота задается следующей последовательностью:

В результате кодирования эта последовательность преобразуется в такой двоичный текст:

Легко вообразить себе, в какое недоумение привели бы мы робота, снабдив его подобной инструкцией. Куда же ему идти? Ясно, что сначала надо идти прямо. А дальше - свернуть влево или повернуть назад, потом еще раз назад? Впереди же еще большая путаница...

Естественно возразить, что следовало бы отделить одни кодовое слово от другого. Разумеется, это можно сделать, но лишь используя либо паузу между словами, либо специальный разделительный знак, для которого необходимо особое кодовое обозначение. И тот и другой путь приведет к значительному удлинению кодового текста, сводя на нет наше предыдущее "усовершенствование".

Другое дело, если мы будем пользоваться прежними кодовыми обозначениями для сообщений A_i. Тогда последовательность (1) будет закодирована так:

Здесь уже не может быть разночтений. Первое слово 0 - идти прямо, второе слово 110 - свернуть влево, так как в списке кодовых слов не значатся слова 1 и 11. В этом сплошном тексте одно за другим однозначно выделяются кодовые слова, и нет сомнений, что робот найдет правильную дорогу.

Итак, суть проблемы в том, что нужно уметь в любом кодовом тексте выделять отдельные кодовые слова без использования специальных разделительных знаков. Иначе говоря, мы хотим, чтобы код удовлетворял следующему требованию: всякая последовательность кодовых символов может быть единственным образом разбита на кодовые слова. Коды, для которых последнее требование выполнено, называются однозначно декодируемыми (иногда их называют кодами без запятой).

Наиболее простыми и употребимыми кодами без запятой являются так называемые префиксные коды, обладающие тем свойством, что никакое кодовое слово не является началом (префиксом) другого кодового слова. Если код префиксный, то, читая кодовую запись подряд от начала, мы всегда сможем разобраться, где кончается одно кодовое слово и начинается следующее. Если, например, в кодовой записи встретилось кодовое обозначение 110, то разночтений быть не может, так как в силу префиксности наш код не содержит кодовых обозначений 1, 11 или, скажем, 1101. Именно так обстояло дело для рассмотренного выше кода, который очевидно является префиксным.

Нетрудно понять, как отражается свойство префиксности или его отсутствие на кодовом дереве. На рис. 6 представлено дерево для кода из таблицы 11 (кружками, как и раньше, помечены те вершины, которые соответствуют кодовым словам). Таким образом, если свойство префикса не выполняется, то некоторые промежуточные вершины дерева могут соответствовать кодовым словам. Для кода Фано это невозможно, так как по самому алгоритму кодирования построение кодового слова заканчивается одновременно с достижением концевой вершины, Следовательно, код Фано является префиксным кодом.

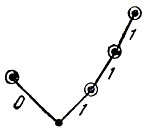
Рис. 6