Характеристические примеры

Полуплоскость. На рис. 6 приведен пример замощения полуплоскости парой полимино. В то же время легко убедиться, что ни квадранта, ни полосы этими полимино замостить нельзя, ибо у замощенной области невозможно обеспечить наличие двух строго прямолинейных границ. Тем самым устанавливается, что из замощаемости полуплоскости не следует замощаемость, скажем, квадранта.

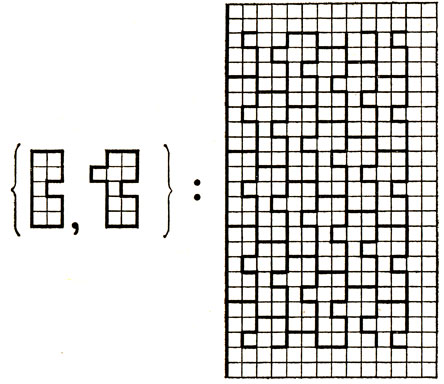
Рис. 6. Характеристический пример для полуплоскости

Квадрант. На рис. 7 показано замощение квадранта с помощью набора из двух полимино. Легко показать, что этот набор полимино не позволяет замостить полосу, так что его можно считать характеристическим для квадранта.

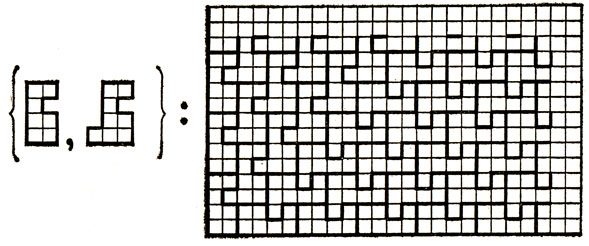
Рис. 7. Характеристический пример для квадранта

Квадрант и полоса. На рис. 8 и 9 показаны замощения квадранта и полосы с помощью набора из двух полимино (в обоих случаях для замощения полосы реально использовано лишь одно полимино).

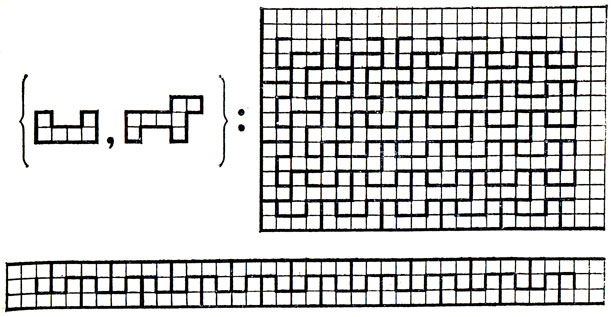
Рис. 8. Характеристический пример для квадранта и полосы: 'собака' и 'корыто'

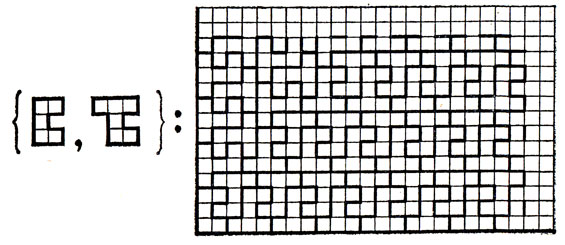
Рис. 9. Характеристический пример для квадранта и полосы: U-пентамино и 'стул'

Для фигурирующего на рис. 8 набора несложно показать, что с его помощью нельзя покрыть угловой полосы; следовательно, этот набор можно считать характеристическим именно для квадранта и полосы. По-видимому, то же можно сказать и о приведенном на рис. 9 наборе, хотя здесь не так просто убедиться в невозможности замощения с его помощью угловой полосы.

Полуполоса. На рис. 10 изображено замощение полуполосы с помощью одного U-пентамино и бесконечного ряда одинаковых "вилкообразных" гексамино. Невозможность замощения прямоугольника этим набором полимино почти очевидна: мы не сможем обеспечить у замощаемой фигуры третьей прямолинейной стороны.

Рис. 10. Характеристический пример для полуполосы

На рис. 11 полуполоса шириной в 6 единиц (равных стороне образующего полимино квадрата) замощена с помощью единственного гептамино. При этом нетрудно установить, что подобное замощение иным способом осуществить нельзя, откуда сразу следует, что этим гептамино нельзя замостить прямоугольник со стороной в 6 единиц. Однако пока никому не удалось доказать, что с помощью этого гептамино (или любого другого полимино, которым можно замостить полуполосу) нельзя замостить никакого прямоугольника.

Рис. 11. Замощение полуполосы единственным гептамино