Замощаемость наборами полимино и способность к самовоспроизводимости

Пусть S - конечный набор полимино. Область R мы будем называть замощаемой набором S, если, выбрав какое-то число экземпляров каждого из входящих в набор S полимино, сможем составить из этих экземпляров рассматриваемую область S. При этом подразумевается, что все используемые полимино имеют один и тот же масштаб, то есть составлены из квадратов одного размера, однако их можно как угодно поворачивать, параллельно переносить, переворачивать (зеркально отображать). Число используемых экземпляров каждого из входящих в набор S полимино может быть различным; для отдельных полимино оно может равняться нулю, что означает отказ от использования именно этого полимино; если область R бесконечна, то и число экземпляров хоть одного из полимино должно быть бесконечным.

Очевидно, что если данным набором полимино можно замостить квадрант (то есть четверть плоскости), то им можно замостить также полуплоскость и всю плоскость; однако из замощаемости, скажем, полуплоскости замощаемость квадранта не вытекает. Эти соображения приводят к установлению определенной иерархии областей R, более подробно обсуждаемой в работе [19].

Пусть набор S полимино таков, что каждое из входящих в S полимино, рассматриваемое как плоская область, может быть замощено с помощью полимино из набора S; в таком случае про S мы будем говорить, что этот набор обладает слабой способностью к самовоспроизводимости. (Разумеется, при этом предполагается, что каждая из рассматриваемых областей составляется из числа полимино, большего единицы.) Это определение не требует, чтобы масштаб каждой подобной одному из полимино области был одним и тем же: возможно, что для того, чтобы замостить подобную полимино А область, А надо увеличить в одно число раз, а для того, чтобы замостить подобную В область, полимино В надо увеличить в иное число раз. Если с помощью набора S можно замостить области, подобные всем входящим в S полимино, взятые в одном и том же масштабе, то про S говорят, что набор S обладает сильной способностью к самовоспроизводимости. Конечно, термин "способность к самовоспроизводимости" на самом деле уместен лишь по отношению к тому, что мы назвали "сильной способностью", ибо только в этом случае процесс воспроизводимости полимино можно неограниченно продолжать. В самом деле, если S обладает лишь слабой способностью к самовоспроизводимости, то может случиться так, что для замощения подобной полимино А области приходится использовать полимино В и С, которые уже нельзя считать полученными в результате подобного процесса из "меньших" полимино: сложить из полимино из набора S можно подобные В и С области, имеющие разный масштаб, тогда как используемые для замощения А полимино должны иметь одинаковый масштаб. Поэтому впредь, употребляя термин "способность к самовоспроизводимости", мы всегда, если только не оговорено противное, будем иметь в виду именно "сильную" способность.

Ясно, что если с помощью полимино из набора S можно замостить некоторый прямоугольник, то стороны этого прямоугольника будут складываться из конечного числа образующих наши полимино квадратов и поэтому будут соизмеримы. А в таком случае нашими прямоугольниками можно замостить квадрат, и, значит, из полимино из набора S можно сложить не только прямоугольник, но и квадрат. Последнее же в свою очередь означает, что набор S полимино обладает способностью к самовоспроизводимости (ибо все полимино складываются из одинаковых квадратов!). Таким образом, из замощаемости прямоугольника следует замощаемость квадрата, а из последней - способность к самовоспроизводимости (рис. 1). С другой стороны, можно доказать, что из способности к самовоспроизводимости уже вытекает замощаемость квадранта [19]. Таким образом, мы приходим к изображенной на рис. 1 иерархии замощаемых областей, причем эта схема содержит всего две нетривиальные импликации: в специальном доказательстве [19] нуждаются лишь утверждения о том, что из замощаемости угловой полосы^* следует замощаемость полосы и что из способности к самовоспроизводимости следует замощаемость квадранта. При этом замощаемость квадранта можно вывести лишь из сильной способности к самовоспроизводимости. Впрочем, до сих пор, кажется, не известен ни один конкретный набор полимино, обладающий слабой способностью к самовоспроизводимости, но не обладающий сильной способностью. Если подобный набор полимино в действительности существует, то даже не ясно, можно ли им покрыть всю плоскость! Этим объясняется место, отведенное на рис. 1 слабой способности к самовоспроизводимости.

^* (Так автор называет объединение двух перекрывающихся взаимно перпендикулярных полуполос, имеющих один общий угол)

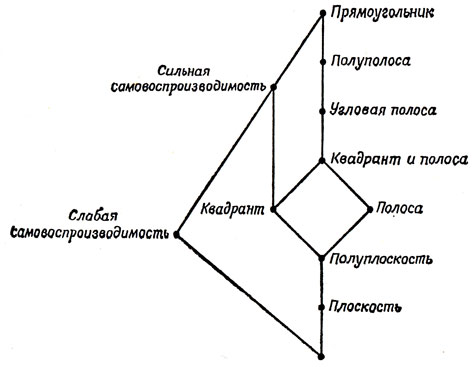
Рис. 1. Иерархия возможностей замощаемости наборами полимино

На рис. 2 приведен пример набора полимино, обладающего способностью к самовоспроизводимости. Этот пример нетривиален, ибо ни одно из входящих в набор полимино само по себе способностью к самовоспроизводимости не обладает. Нетрудно видеть, что этот набор полимино позволяет замостить прямоугольник.

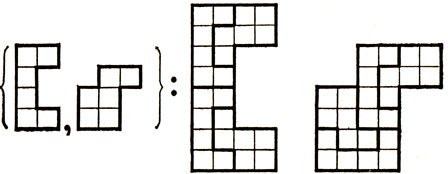
Рис. 2. Набор из двух гексамино, обладающий способностью к самовоспроизводимости

На рис. 3 изображен еще один набор из двух полимино, который обладает способностью к самовоспроизводимости, в то время как ни одно из входящих в набор пентамино этой способностью не обладает. В самом деле, поскольку, как показано на рис. 3, из наших пентамино можно сложить квадрат размером 10×10, то из них можно также сложить каждое из входящих в набор пентамино, увеличенное в 10 раз в каждом измерении. Мы предоставляем читателю возможность попытаться самостоятельно выяснить, из каких вообще пар пентамино можно сложить квадрат.

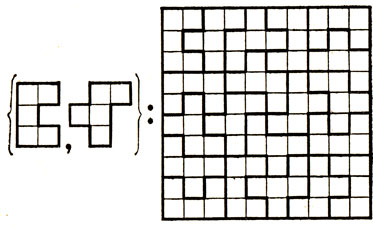
Рис. 3. Набор из двух пентамино, позволяющий замостить квадрат

На рис. 4 приведен интересный пример, показывающий существенную зависимость замощаемости данным набором полимино от требования, чтобы все полимино брались в одном и том же масштабе. Три изображенных на рисунке гексамино позволяют замостить прямоугольник, откуда следует, что рассматриваемый набор полимино обладает способностью к самовоспроизводимости. Однако с помощью двух из рассматриваемых гексамино можно замостить третье! Из сказанного вовсе не следует, что набор из двух гексамино обладает хотя бы слабой способностью к самовоспроизводимости, поскольку здесь уже на первой стадии процесса воспроизводимости полимино нам придется использовать гексамино разного масштаба.

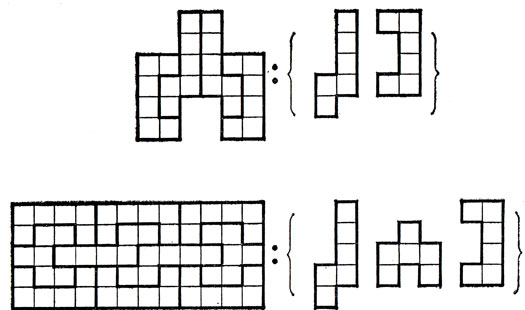
Рис. 4. Набор из трех гексамино, которыми можно замостить прямоугольник, причем из двух гексамино можно составить третье. Набор из двух гексамино не обладает способностью к самовоспроизводимости

Упомянем еще о понятии "способность к правильной самовоспроизводимости (порядка k)". Оно означает, что область, подобную каждому из входящих в рассматриваемый набор полимино, можно составить, используя по k экземпляров каждого полимино из нашего набора (то есть одно и то же число каждого из полимино!). Так, на рис. 5, заимствованном из статьи М. Гарднера [1 ж] (который в этой связи ссылается на английского ученого М. Дж. Поваха), изображен набор из четырех гексамино, обладающий способностью к правильной самовоспроизводимости первого порядка. (В той же статье указаны еще два набора, которые обладают способностью к правильной самовоспроизводимости первого порядка: один из них состоит из черырех октамино, а второй - из четырех "тетраболо", треугольных монстров, составленных из четырех треугольников каждый.)

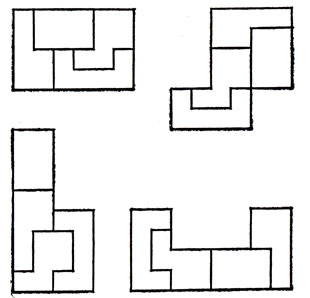
Рис. 5. Набор из полимино, обладающий способностью к правильной самовоспроизводимости первого порядка