Покрытия прямоугольников конгруэнтными n-мино. Д. А. Клэрнер

(Кlаrnеr D. A., Packing a Rectangle with Congruent N-ominoes, J. Combinatorial Theory, 7, № 2, 107-115 (September 1969).)

Квадратная сетка состоит из узлов, ребер и клеток. Узлами сетки являются все точки, имеющие в заданной на плоскости декартовой прямоугольной системе координат целочисленные координаты; ребра - отрезки, соединяющие соседние узлы сетки, а клетки - единичные квадраты, на которые разбивают плоскость ребра сетки, n-мино - это объединение n клеток сетки, которое не распадается на отдельные части и которое нельзя разбить на части удалением отдельных вершин (а лишь удалением целых ребер сетки).

Мы будем говорить, что n-мино X может покрыть (или заполнить) прямоугольник R размером a×b, если R можно разбить на непересекающиеся (не имеющие общих внутренних точек) части Х₁, Х₂, ..., конгруэнтные X. Если в этом покрытии участвуют k копий X (то есть если площадь R равна kn), то мы будем говорить, что рассматриваемое покрытие имеет кратность k. Совокупность кратностей покрытий конгруэнтными Х-полимино всевозможных прямоугольников R условимся обозначать через Р(X); если с помощью X нельзя покрыть никакого прямоугольника, будем писать Р(X) = ø^*. Поскольку из k ∈ Р(X), очевидно, следует, что и jk ∈ P(X) (где j = 1, 2, 3, ... ), то множество Р(X) либо пусто, либо бесконечно. Наименьшее из входящих в множество Р(X) чисел мы будем обозначать через р(X) и называть порядком n-мино X. Ясно, что р(X) = 1 в том и только в том случае, если X - прямоугольник. Верно ли, что если р(X) нечетно, то р(X) = 1 (и, значит, X - прямоугольник)? Вопрос этот представляется вовсе не простым.

^* (Символом ø в математике обозначается так называемое пустое множество, не содержащее ни одного элемента.)

Легко охарактеризовать и все n-мино второго порядка [все n-мино X, для которых р(X) = 2]. Прямоугольник R размером а×b, где аb = 2n, можно разрезать на два конгруэнтных n-мино, проведя образованную ребрами сетки ломаную, соединяющую две противоположные стороны R и симметричную относительно центра R. Пересчитав все ломаные такого рода, мы найдем число всех n-мино второго порядка.

Кажется очевидным, что n-мино третьего порядка вовсе не существует: если 3 ∈ Р(X), то р(X) = 1; иными словами, прямоугольник можно покрыть тремя конгруэнтными n-мино лишь в том случае, если эти n-мино прямоугольники. Идея возможного доказательства этого интуитивно ясна, однако привести точное доказательство, видимо, не легко. Было бы интересно выяснить также, возможно ли разбить какой-либо прямоугольник на три любые (но не прямоугольные!) конгруэнтные части Х₁, Х₂ и Х₃ (разумеется, не имеющие общих внутренних точек).

Дать исчерпывающее описание всех полимино четвертого порядка, вероятно, достаточно трудно. Кажется правдоподобным, что каждое полимино четвертого порядка должно принадлежать к одному из двух описываемых ниже классов; однако, даже если это утверждение справедливо, вряд ли существует достаточно простое его доказательство.

Обозначим через S_g^h ступенчатое N-мино (или N-лестницу) с h ступенями высоты g; площадь N этого N-мино, очевидно, равна

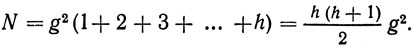
Ясно что S_g^h подобно (в смысле элементарной геометрии) n-мино S₁^h, составленному из первых h клеток квадратной сетки, расположенных в 1-й строке справа от оси ординат, первых h - 1 клеток 2-й строки, ..., первой клетки h-й строки; здесь n = [h (h + 1) 1/2. Аналогично через S_g^h + S_i^j обозначим объединение зеркального образа S_g^h, получаемого отражением S_g^h от оси ординат, и S_i^j. На рис. 1 изображены S₁³, S₁³ + S₂¹ и прямоугольник размером 5×8, покрытый четырьмя копиями S₁³ + S₂¹.

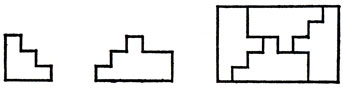
Рис. 1

Двумя экземплярами S^v_u можно покрыть прямоугольник размером uv×(uv + u), который мы будем обозначать через R (S^v_u). Если одна из сторон прямоугольника R (S^j_i) имеет ту же длину, что и одна из сторон R (S^h_g), то четырьмя экземплярами S^j_i + S^h_g можно покрыть некоторый прямоугольник. Например, если ij = gh + g, мы можем разрезать прямоугольник R размером (ij + gh + g) × (ij + gh + i) на два экземпляра R (S^j_i) и два экземпляра R (S^h_g) так, чтобы получающаяся в результате конфигурация была симметрична относительно центра исходного прямоугольника R. Если экземпляры S^j_i и S^h_g, используемые для покрытия прямоугольников R (S^j_i) и R (S^h_g), получаются из ступенчатого полимино S^v_u поворотом (но не отражением - то есть их не приходится переворачивать), то связанная с R конфигурация может быть изменена хаким образом, что из нее получится прямоугольник, покрываемый четырьмя экземплярами S^j_i + S^h_g. Разумеется, полимино S^j_i + S^h_g не обязательно имеет четвертый порядок - его порядок может равняться двум; однако нетрудно установить накладываемые на числа i, j, g и h условия, при выполнении которых этот порядок равен именно четырем. Описанная конструкция (где i = j = 2, g = 1 и h = 3) изображена на рис. 2.

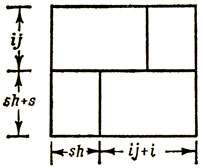
Рис. 2

Элементы другого класса полимино четвертого порядка (частично, возможно, пересекающегося с первым классом) можно получить с помощью разбиения квадрата размером 2j × 2j (j = 2, 3, ...) на четыре конгруэнтных n-мино, получаемых поворотами на 0, 90, 180 и 270° некоторой образованной ребрами квадратной сетки ломаной, выбранной так, что итоговая конфигурация оказывается симметричной относительно центра квадрата. Пример n-мино этого типа приведен на рис. 3.

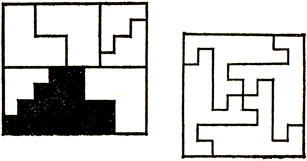
Рис. 3

Существуют ли полимино, порядок которых отличен от 1, 2 и 4? Все известные нам примеры исчерпываются изображенными на рис. 4-7 пентамино порядка 10, гексамино порядка 18, гептамино порядка 28 и октамино порядка 24. На всех рисунках не покрытая полимино часть (или части) прямоугольника конгруэнтна покрытой части; следовательно, они могут быть покрыты аналогично области, разбитой на полимино.

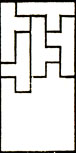
Рис. 4

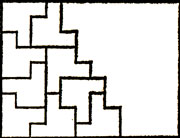
Рис. 5

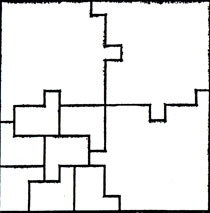
Рис. 6

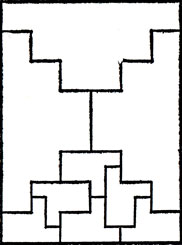
Рис. 7

Если множество Р(X) содержит лишь четные числа то полимино X мы назовем четным; в противном случае (то есть если существует хоть один прямоугольник R, кратность покрытия которого конгруэнтными X полимино нечетна) назовем X нечетным. Интересно было бы выяснить условия, позволяющие для каждого заданного полимино определить, является ли оно четным или нечетным, но пока мы еще очень далеки от решения этой задачи. Можно лишь доказать, что оба рассматриваемых класса содержат бесконечно много различных полимино.

Теорема 1. Существует бесконечно много попарно не подобных непрямоугольных^* нечетных полимино.

^* (Разумеется, каждое прямоугольное полимино нечетно, ибо его порядок равен 1.)

Доказательство. Прямоугольник R размером 5×9, изображенный на рис. 8, покрыт 15 L-тримино, из чего сразу следует, что это тримино нечетное. Если растянуть R в а раз по вертикали ив b раз по горизонтали, он перейдет в прямоугольник размером 5а × 9b, покрытый 15 3ab-мино, конгруэнтными изображенному на рис. 9. Обозначим это 3ab-мино через Х^b_а. Очевидно, что Х^b_а нечетно [поскольку, например, 15 ∈ Р (Х^b_а)]. Если мы теперь ограничимся лишь взаимно простыми а и b, причем потребуем еще, чтобы было а < b, то придем к бесконечному множеству нечетных полимино, ни одно из которых не будет подобно ни одному другому.

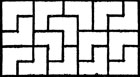
Рис. 8

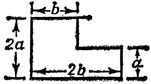
Рис. 9

Кажется довольно неожиданным, что 11 X²₁ можно покрыть прямоугольник, однако такое покрытие существует: оно изображено на рис. 10. Нам не известен ни один пример непрямоугольного полимино, которым можно покрыть прямоугольник с кратностью покрытия меньшей 11; более того, мы не знаем ни одного отличного от X²₁ и от прямоугольника полимино, которым можно покрыть прямоугольник с кратностью 11. Не равна ли 11 наименьшая возможная нечетная кратность покрытия прямоугольника непрямоугольным n-мино? Ответ на этот вопрос нам неизвестен.

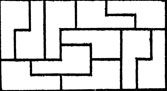
Рис. 10

На рис. 11 и 12 приведены два примера нечетных пентамино; решить вопрос о том, четно или нечетно изображенное на рис. 4 пентамино, мы так и не смогли. Мы не знаем также ни одного отличного от изображенных на рис. 11 и 12 полимино и от бесконечной серии полимино Х^b_а [где а, b = 1, 2, 3, ...], про которое было бы точно известно, что оно нечетно, хоть вполне возможно, что найти другие примеры вовсе не так трудно.

Рис. 11

Рис. 12

Нетрудно построить n-мино второго порядка, наверняка являющееся четным: этого можно достичь, специальным образом сочленяя n-мино само с собой. Однако более удовлетворительным кажется способ доказательства существования бесконечного множества четных полимино, базирующийся на следующей теореме.

Теорема 2. Пусть клетки квадратной сетки раскрашены в белый и черный цвета в шахматном порядке, и пусть некоторое 2n-мино X состоит из k черных и 2n - k белых клеток, где k ≠ n. Тогда, если с помощью X можно покрыть хоть один прямоугольник, полимино X четное.

Доказательство. Пусть прямоугольник R покрыт h экземплярами X₁, X₂, ..., X_h, удовлетворяющего условиям теоремы 2n-мино X. Разобьем совокупность этих h полимино на две части, S и Т, отнеся к S все X_i (i = 1, 2, ..., h), состоящие из k черных и 2n - k белых клеток, а к T - полимино Х_i, состоящие из 2n - k черных и k белых клеток; количество полимино в множествах S и Т обозначим через |S| и |Т|. Поскольку площадь прямоугольника R равна 2nh, этот прямоугольник состоит из nh черных и nh белых клеток. Каждое полимино из S покрывает k черных клеток, и каждое полимино из T покрывает 2n - k черных клеток. А так как все полимино из совокупностей S и Т вместе покрывают все черные клетки прямоугольника R, то

Аналогично число белых клеток прямоугольника R равно

Следовательно,

в силу чего (поскольку k ≠ n) |S| = |T|, так что

очевидно, является четным.

На рис. 13 изображено семейство 4n-мино Y₁, Y₂, ..., попарно не подобных друг другу и удовлетворяющих условиям теоремы 2. Этот пример служит доказательством того, что справедлива

Рис. 13

Теорема 3. Существует бесконечно много попарно не подобных четных полимино.

Другое (бесконечное) семейство четных 2n-мино, не охватываемое теоремой 2, может быть найдено с помощью следующей теоремы.

Теорема 4. Пусть столбцы клеток квадратной сетки последовательно окрашены в черный и белый цвета и пусть X - такое 2n-мино, что каждое конгруэнтное ему 2n-мино состоит либо из k черных и 2n - k белых клеток, либо, наоборот, из 2n - k черных и k белых клеток, где k ≠ n. Тогда, если с помощью X можно покрыть хоть один прямоугольник, полимино X четное.

Доказательство. Пусть прямоугольник R покрыт h экземплярами X₁, X₂, ..., X_h, удовлетворяющего условиям теоремы 2n-мино X. Мы всегда можем считать R расположенным так, что он покрывает nh черных и nh белых клеток. Разобьем теперь h полимино Х₁, Х₂, ..., X_h на два класса, S и Т, отнеся к первому из них те полимино, которые покрывают k черных клеток, а ко второму - полимино, покрывающие k белых клеток. Рассуждая далее в точности как при доказательстве теоремы 3, мы заключим, что |S| = |Т| и что число h = |S| + |T| = 2 |S| четное.

Каждое из изображенных на рис. 14 4n-мино Z₁, Z₂, ... удовлетворяет условиям теоремы 4 (но ни одно из них не удовлетворяет условиям теоремы 2!), поэтому все эти полимино являются четными. А так как никакие два из полимино Z₁, Z₂, Z₃, ... не подобны друг другу,то из рис. 14 следует еще одно доказательство теоремы 3. Изображенное на рис. 5 гексамино также удовлетворяет условиям теоремы 4, поэтому и оно является четным. Вполне возможно, что это гексамино даже таково, что кратности покрытий с его помощью любых прямоугольников все делятся на 4, а может быть, даже на 8.

Рис. 14

Имеется несколько теорем, характеризующих прямоугольники, покрываемые конкретными полимино X. Простейший случай - когда X само есть прямоугольник - исследован до конца.

Теорема 5. Прямоугольник R размером а×b может быть покрыт прямоугольниками размером 1×d в том и только в том случае, если на d делится а или b.

Доказательство. Если а или b делится на d, то прямоугольник R, очевидно, может быть разбит на (1×d)-прямоугольники.

Предположим теперь, что (а×b)-прямоугольник R покрыт прямоугольниками 1×d, и пусть а = qd + r, где 0 < r < d. Перпендикулярные стороне длиной а (которую мы будем считать горизонтальной) ряды клеток занумеруем слева направо числами 1, 2, ..., а и затем начнем их последовательно красить в d цветов f₁, f₂, ... f_d, при этом m-й столбец получит цвет f_i, где m = i → (mod d). Если l_i - число клеток прямоугольника R, закрашенных цветом f_i, то при 1 ≤ i ≤ r имеем l_i = qb + b, а если r + 1 ≤ i ≤ d, то l_i = qb. Пусть х - число "горизонтальных" прямоугольников размером 1×d, содержащих в точности по одной клетке каждого из цветов f_i, а у - число "вертикальных" прямоугольников, состоящих из d клеток одного цвета. При этом положим у = у₁ + у₂ + ... + y_d, где y_i - число прямоугольников, целиком окрашенных цветом f_i (здесь i = 1, 2, ..., d). А так как l_i = х + dy_i, то имеем

здесь i, j = 1, 2, ..., d любые и i ≠ j. В частности,

так что b ≡ 0 (mod d), то есть делится на d.

Следствие. Прямоугольник R размером а×b можно покрыть прямоугольниками размером с×d, в том и только в том случае, если а или b делится на с и а или b делится на d, причем если и на с, и на d делится одна из сторон прямоугольника R, а вторая не делится, то другая сторона имеет вид сх + dy, где х и у - целые неотрицательные числа.

Доказательство. Если, скажем, а делится на с, a b делится на d, то прямоугольник R размером а×b очевидным образом может быть разбит на прямоугольники размером с×d. Если а делится и на cd, и на ab = сх + dy, где х и у - целые положительные числа, то прямоугольник R можно разрезать на х полос размером с×d и у полос размером d×а, каждую из которых можно разбить на прямоугольники размером с×d.

Пусть теперь прямоугольник R размером а×b разбит на (с×d)-пpямoyгoльники. Поскольку каждый (с×d)-прямоугольник можно разбить на (1×d)-пoлocы, то, в силу теоремы 5, отсюда вытекает, что а или b делятся на d; точно так же показывается, что а или b делятся на с. Наконец, каждая сторона прямоугольника R состоит из ряда отрезков длин end примыкающих к ней сторон (с×d)-прямоугольников, то есть она может быть представлена в виде сх + dy, где х, у ≥ 0. Отсюда и вытекает требуемое утверждение.

Задача полной характеризации всех прямоугольников, покрываемых с помощью n-мино второго порядка X, представляется безнадежно трудной. Даже если мы ограничимся лишь (простейшими после прямоугольных!) L-образными n-мино второго порядка, то и тогда искомая теорема будет, по-видимому, слишком запутана, чтобы ее можно было бы сформулировать разумным образом. Ясно, что если n-мино X сочетается само с собой некоторым сложным способом, образуя прямоугольник r размером с×d, то X покрывает прямоугольник R, когда R можно разбить на равные r части; однако не ясно, какой точный смысл следует придать здесь выражению "сочетается сложным способом".

С. Голомб в статье [8] утверждает, что можно найти необходимое и достаточное условие того, чтобы L-тетрамино (наименьшее из изображенных на рис. 14 полимино) покрывало прямоугольник размером а×b. Автор настоящей статьи и другие исследователи показали, что L-тетрамино покрывает прямоугольник размером а×b тогда и только тогда, когда а,b > 1 и ab делится на 8. Валкуп в статье [9^*] доказал, что Т-тетрамино покрывает прямоугольник а×b тогда и только тогда, когда а и b делятся на 4; возможно, что его метод может быть также применен для доказательства того, что изображенное на рис. 4 пентамино покрывает некоторый прямоугольник в том и только в том случае, если одна сторона этого прямоугольника делится на 5, а другая - на 10. Из этого следовало бы, что Y-пентамино (с помощью которого, как нетрудно показать, можно покрыть любой прямоугольник размером 16×5m и любой прямоугольник размером 24×5m, где m = 2, 3, 4, ...) есть четное полимино, но пока этот вопрос остается открытым.

Приведем в заключение еще одну теорему такого рода.

Теорема 6. Прямоугольник R размером а×b в том и только в том случае можно покрыть с помощью изображенного на рис. 14 Р-октамино, если а,b > 3 и ab делится на 16.

Доказательство. Если а,b > 3 и ab делится на 16, то прямоугольник R размером а×b можно разрезать на прямоугольники, размеры которых указаны на рис. 15.

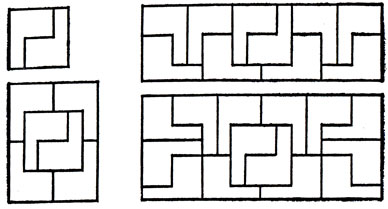
Рис. 15

Пусть теперь мы имеем прямоугольник R размером а×b, покрытый с помощью k экземпляров Р-октамино; в таком случае ab = 8k. Чтобы показать, что ab делится также и на 16, достаточно убедиться, что наше полимино четное. Поскольку ab делится на 8, одна из сторон прямоугольника R - скажем, сторона а - делится на 4. Будем считать эту сторону горизонтальной и занумеруем а столбцов клеток рассматриваемого прямоугольника числами 1, 2, ..., а; затем закрасим m-й столбец в красный цвет, если m ≡ 1 (mod 4), в белый цвет, если m ≡ 2, 4 (mod 4), и в синий цвет, если m ≡ 3 (mod 4). Будем говорить, что покрывающее R Р-октамино имеет тип (х, у, z), если оно состоит из х красных, у белых и z синих клеток. Обозначим теперь через S₁, S₂, S₃, S₄, S₅ и S₆ соответственно множества Р-октамино из покрытия типов (3, 4, 1), (1, 3, 4), (4, 2, 2), (2, 6, 0), (2, 2, 4) и (0, 6, 2). Легко удостовериться в том, что произвольное Р-октамино из данного покрытия непременно относится к одному из этих типов. Поскольку же число синих клеток в R равно числу красных клеток, то мы имеем

откуда

Таким образом, в покрытии использовано всего

Р-октамино; следовательно, это октамино четное.