Нерешенные задачи

Последующие задачи никем не решены, но их неразрешимость также пока не доказана. В задачах предполагается, что речь идет о покрытиях при помощи пентамино.

81.

82.

83.

В задачах 24-25 представлены единственно известные сейчас результаты, относящиеся к проблеме одновременного построения нескольких прямоугольников из пентамино (так, что ни одно пентамино не используется дважды). Кроме того, известно, что нельзя одновременно построить прямоугольники размерами 3×10 и 6×5 (задача 76); нельзя сложить прямоугольник размером 3×20 из двух меньших (задача 79), и нельзя сложить одновременно прямоугольники размерами 2×10 и 4×10. Задачи 84-87 предлагают другие конструкции, которые, возможно, окажутся разрешимыми.

84. Сложите из пентамино прямоугольники размерами 4×5 и 5×8.

85. Постройте одновременно два прямоугольника размерами 3×5 и 5×9.

86. Требуется построить из одного набора пентамино прямоугольники размерами 4×5 и 4×10.

87. Та же задача для прямоугольников размерами 2×10 и 5×8.

88. Задача 15 квадратов. Существует ли укладка трех пентамино, которую можно повторить четыре раза, используя один набор пентамино? (Ср. с задачами 33-34.)

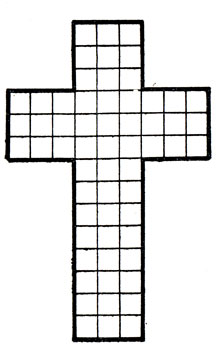
89. Из прямоугольника размером 3×20 можно попытаться образовать много схожих фигур. Показанный здесь крест - лишь одна из представляющихся возможностей.

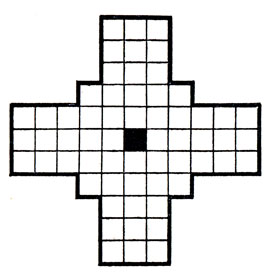
90. Другая такая возможность - крест с отверстием посередине.

91. Известно, что девяти пентамино достаточно, чтобы утроить любое данное пентамино (см. задачу 37). А можно ли с помощью девяти наборов пентамино утроить все фигуры обычного набора пентамино?

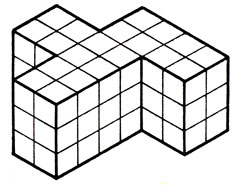
92. Можно ли из 12 пространственных пентамино построить показанную здесь модель F-пентамино? (см. задачу 46).

Несомненно, читатель сможет и сам найти новые задачи, относящиеся к плоским и пространственным полимино. Так, например, материал гл. VII представляет собой практически не изученную область, в которой возникает великое множество задач.