Невозможные конструкции

В следующих задачах представлены "доски", которые нельзя покрыть 12 пентамино. Для тех задач, которые отмечены звездочками, до сих пор не найдено достаточно простого доказательства их неразрешимости.

71^*.

72^*.

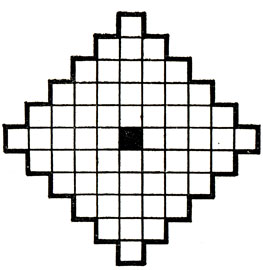
73.

74.

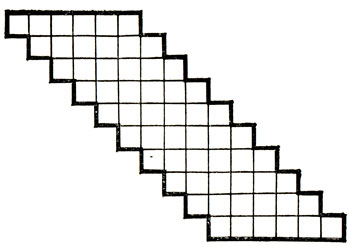
75^*.

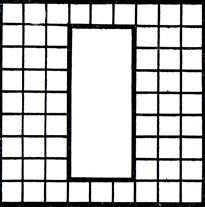
76^*.

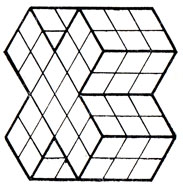
77^*. Требуется доказать невозможность построения из 12 пространственных пентамино.

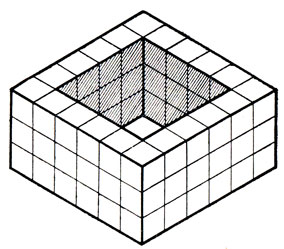
78. Невозможно построить из 12 пространственных пентамино.

79^*. Прямоугольник размером 3×20, заполненный 12 пентмино, нельзя составить из двух меньших прямоугольников.

80. Положите на шахматную доску размером 8×8 четыре мономино произвольным образом, но так, чтобы они не отделяли изолированной части доски. Покажите, что оставшуюся часть доски нельзя покрыть 12 пентамино.