Прямоугольники из домино

Другой тип задач о полимино сводится к нахождению математических выражений для числа способов, которыми из заданного набора полимино можно сложить ту или иную наперед заданную конфигурацию. Несомненно, в общем случае такая задача невероятно трудна. Однако в одном частном случае ответ получается сравнительно легко, причем вывод требуемого выражения оказывается довольно элегантным. К рассмотрению этой частной задачи мы и перейдем.

В майском номере журнала American Mat hematic Monthly за 1961 год У. Е. Пэттон предложил следующую задачу: требуется построить из прямоугольников размером 1×2 (из домино) прямоугольник размером 2×n или, другими словами, требуется покрыть этот прямоугольник домино. Сколькими способами это можно сделать, если считать разными случаи, не переводимые друг в друга движениями (поворотами и зеркальными отражениями)?

В январском номере этого же журнала за 1962 год было опубликовано решение задачи Пэттона, принадлежащее автору.

Сначала подсчитаем число возможных укладок домино в прямоугольник размером 2×n, не учитывая требуемого отождествления симметричных укладок. При n = 1 число возможных укладок f₁ = 1. При n = 2 два домино можно расположить как горизонтально, так и вертикально; таким образом, число укладок в этом случае f₂ = 2. Рассматривая случай n > 2, заметим, что либо слева расположено одно вертикальное домино - и тогда число способов заполнить весь прямоугольник равно f_n-1, либо слева лежат два горизонтальных домино - и тогда число способов заполнить оставшуюся часть прямоугольника равно f_n-2. Следовательно, f_n = f_n-1 + f_n-2, что иллюстрируется рис. 144.

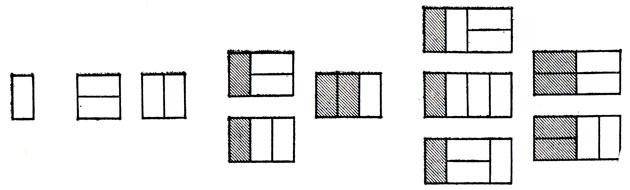
Рис. 144. Покрытие прямоугольника 2×n домино для n = 1, 2, 3 и 4

Последовательность, начинающаяся с элементов f₁ = 1 и f₂ = 2 и при n > 2 удовлетворяющая условию f_n = f_n-1 + f_n-2, есть знаменитая последовательность Фибоначчи^*:

^* (Ср., например, Н. Н. Воробьев, Числа Фибоначчи, М., изд-во "Наука", 1964.)

Леонардо Фибоначчи (известный также под именем Леонардо Пизанского) - итальянский математик XIII века, впервые познакомивший математический мир с этой последовательностью. Правда, у Фибоначчи последовательность начиналась с чисел 0 и 1, но каждый последующий член, как и у нас, образовывался сложением двух предыдущих, так что у него последовательность имела вид: 0, 1, 1, 2, 3, 5, 8, 13, ...

Обозначим теперь через С_m число укладок прямоугольника 2×m, причем таких, что укладки, получающиеся одна из другой зеркальной симметрией, не считаются различными. Тогда С_m = ¹/₂ (f_m + s_m), где через s_m обозначено число симметричных укладок, переводимых зеркальной симметрией в себя. Это выражение представляет собой непосредственный пример применения формулы N = ¹/₂ (T + С) гл. V, используемой для подсчета числа различных случаев при отождествлении переводимых друг в друга инволюцией вариантов. Можно и непосредственно вывести эту формулу. Действительно, число несимметричных укладок очевидным образом равно f_m - s_m, и лишь половину этого числа следует учитывать среди различных укладок, поскольку мы договорились рассматривать различающиеся укладки "с точностью до симметрии". Напротив, все симметричные случаи различны, и поэтому общее число различных укладок равно

Для того чтобы найти s_m, рассмотрим отдельно случаи нечетного и четного m.

Если m = 2n + 1, то в симметричной укладке центральное место должно занимать вертикальное домино, по бокам которого находятся две укладки размерами 2×n. Одну из них можно составить f_n способами, и в силу симметрии укладка другой этим полностью определяется. Поэтому

Если же m = 2m, то вертикальная прямая, проходящая через центр прямоугольника, либо пересечет пару горизонтально расположенных домино, либо не пересечет ни одного домино. В первом случае левый прямоугольник размером 2×(n - 1) можно заполнить f_n-1 способами; во втором случае левый прямоугольник размером 2×n можно заполнить f_n способами. Как и раньше, укладка левого прямоугольника полностью определяет укладку правого, ибо мы рассматриваем лишь симметричные укладки всего прямоугольника. Следовательно,

Итак,

что полностью решает поставленную выше задачу для всех m, за исключением m = 2, поскольку прямоугольник размером 2×2 суть квадрат и допускает еще и "поворотную симметрию" четвертого порядка (переходит в себя при повороте на 90°). Отсюда следует, что вместо С₂ = 2 следует считать С₂' = 1, сохраняя единственный случай расположения двух домино.

Полученные нами результаты сведены в следующую таблицу.

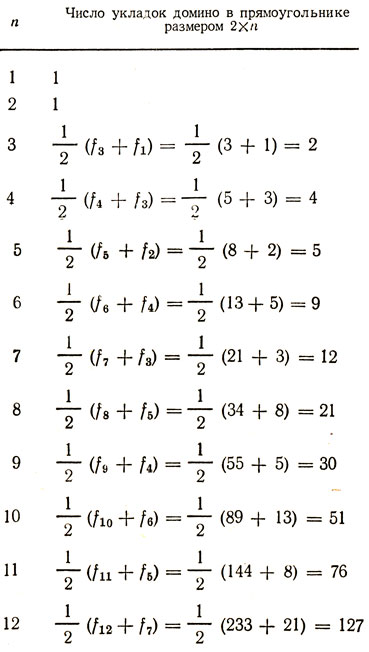
Ясно, что подсчитать число покрытий костями домино прямоугольника размером 3×n значительно труднее. Мы предлагаем читателю испытать свои силы в решении этой задачи. Значительно проще определить число укладок прямоугольника размером 2×n или даже размером 3×n прямыми тримино. Задача же об определении числа укладок прямоугольника размером 4×n прямыми тримино выглядит уже весьма интригующе. Однако, как нам кажется, у решающего ее сохраняются еще неплохие шансы на успех. Заинтересованный читатель может заняться решением этой задачи.

Итак, наша прогулка по увлекательному царству полимино подошла к концу. Не вызывает сомнения, что немало интересного и волнующего мы неизбежно пропустили. Поэтому мы приглашаем читателя почаще возвращаться к полимино и самостоятельно находить новые пути, ибо решение математических задач - неиссякаемый источник наслаждения.