Треугольные и шестиугольные "монстры"

В своих работах о полимино Фрэнк Харари, профессор математики Мичиганского университета, назвал n-мино "монстрами, составленными из n ячеек". В статье "Шахматные доски и полимино" [7], на которую мы уже не раз ссылались, рассматриваются различные покрытия и фигуры, составленные не из квадратов, а из других фигур, скажем из треугольников или шестиугольников. Комбинацию связанных правильных (равносторонних) треугольников можно было бы тогда назвать треугольным монстром, а комбинацию связанных правильных шестиугольников - шестиугольным монстром. На рис. 134 изображены треугольные монстры первого - пятого порядков.

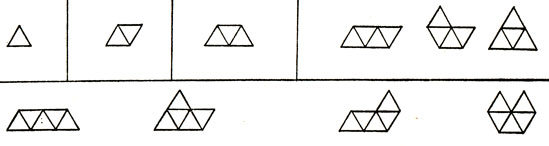
Рис. 134. Треугольные монстры до пятого порядка

Недавно английские математики Дж. Е. Рив и Дж. А. Тиррел опубликовали статью под заголовком "Господин Головоломка" [23]. Под этим названием в Англии выпускаются в продажу различные головоломки, связанные с полимино. В статье изучены различные формы, которые можно составить из всех 12 треугольных монстров шестого порядка. Как сообщили Рив и Тиррел, они нашли свыше 40 решений задачи о покрытии ромба, показанного на рис. 135 (на этом рисунке представлено одно из возможных решений).

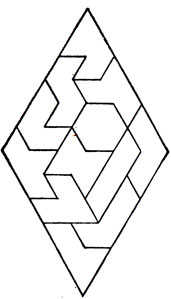
Рис. 135. Покрытие ромба двенадцатью треугольными монстрами шестого порядка

В той же статье [23] рассмотрена задача о покрытии с помощью 9 из 12 треугольных монстров шестого порядка правильного шестиугольника, изображенного на рис. 136. Всего существует С₁₂⁹ = 220 способов отобрать 9 из 12 монстров, причем 90 из них очевидным образом непригодны для покрытия шестиугольника, поскольку в соответствующие им наборы монстров входит лишь один, а не оба "уравновешенных" монстра, изображенных на рис. 137. Так как весь шестиугольник на рис. 136 "уравновешен", то есть содержит столько же белых треугольников, сколько и заштрихованных, то ясно, что его нельзя покрыть никаким набором, содержащим нечетное число "уравновешенных" монстров. Рив и Тиррел утверждают, что 22 из остающихся 130 задач неразрешимы, "но [им] не удалось найти этому простое доказательство". Мы приглашаем читателя попробовать себя на этих задачах, а также исследовать другие интересные формы, заполняемые (или не заполняемые) треугольными монстрами. Например, можно ли семью треугольными монстрами четвертого и пятого порядков заполнить ромб, изображенный на рис. 138?

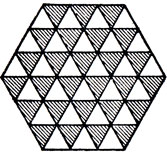
Рис. 136. Правильный шестиугольник

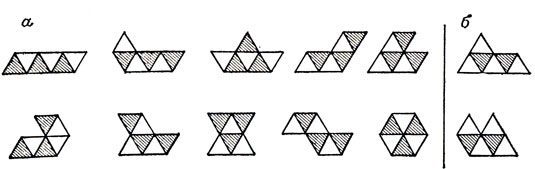
Рис. 137. 'Уравновешенные' и 'неуравновешенные' монстры. а - уравновешенные монстры; б - неуравновешенные монстры

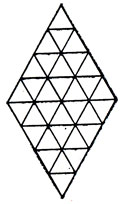
Рис. 138. Ромб

В колонке "Головоломки и парадоксы", которую в английском журнале New Scientist ведет Т. Г. О'Берн, было поставлено великое множество задач, относящихся к треугольным монстрам. О'Берн даже придумал названия 12 треугольным монстрам шестого порядка (рис. 139). Во многих его конструкциях используются 19 таких фигур: в дополнение к обычным 12 он берет 7 зеркальных образов асимметричных монстров. Одна из задач сводится к расположению этих 19 монстров в виде трех шестиугольников, один из которых совпадает с шестиугольным монстром, а два других - с шестиугольником, изображенным на рис. 136. В журнале долгое время обсуждалась также проблема заполнения фигуры в форме пчелиных сот, показанной на рис. 140. На рис. 141 представлены все 24 треугольных монстра седьмого порядка. Читателю предоставляется возможность попробовать сложить из этих монстров что-нибудь интересное.

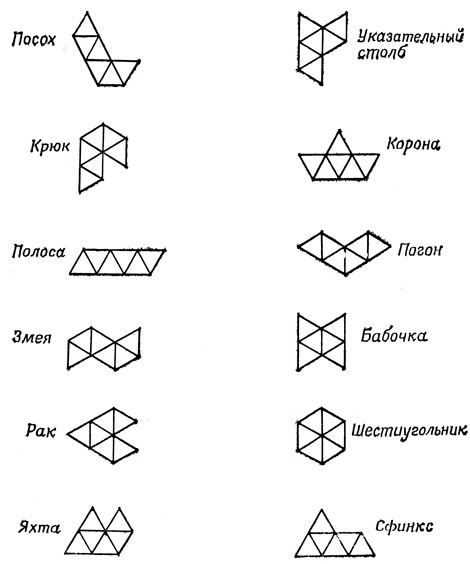
Рис. 139. Треугольные монстры из шести элементов

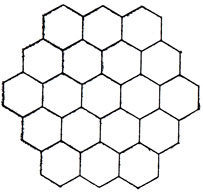
Рис. 140. Пчелиные соты (их можно, псжрыть 19 односторонними треугольными монстрами шестого порядка)

Рис. 141. 24 монстра седьмого порядка

Заполнение плоскости фигурами определенного вида принято называть паркетажем. Если, рассматривая квадратный паркетаж, соединить центры всех соседних квадратов, то построенные отрезки дадут нам новый паркетаж плоскости, отличающийся от исходного лишь сдвигом. Однако если в качестве исходного взять не квадратный, а треугольный паркетаж, то отрезки, соединяющие центры соседних треугольников, образуют шестиугольный паркетаж плоскости. И обратно, отправляясь от шестиугольного паркетажа, мы придем к треугольному. По этой причине треугольный и шестиугольный паркетажи считают взаимно двойственными друг другу, а квадратный паркетаж двойствен самому себе. Как видно из рис. 136, элементы треугольного паркетажа допускают правильную "шахматную" раскраску. Такая раскраска уже невозможна для шестиугольного покрытия плоскости. Тем не менее, используя три цвета, можно правильно закрасить и шестиугольный паркетаж, получив своеобразный шестиугольный аналог шахматной доски. Подобная раскраска приведена на рис. 142.

Рис. 142. Трехцветная раскраска шестиугольников

Простейшие шестиугольные монстры изучались - разумеется, под другим названием - химиками как модели молекулярных структур органических соединений. Шестиугольные монстры, состоящие из 1, 2, 3, 4 или 5 правильных шестиугольников, изображены на рис. 143. Соответствующая проблематика почти не освещалась в литературе, так что читатель может смело вторгаться на не занятую пока никем территорию и попытаться самостоятельно сложить те или иные интересные фигуры из шестиугольных монстров.

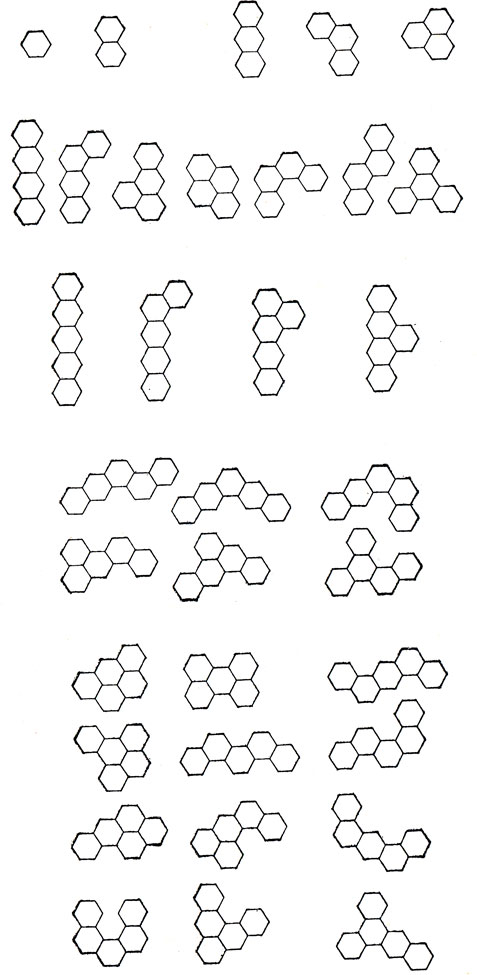
Рис. 143. Шестиугольные монстры до пятого порядка