Псевдо- и квазиполимино

Чтобы обобщить основные понятия полимино, можно пойти на ослабление требования связности соседних квадратов. Обычное полимино, как упоминалось в гл. I, может обойти ладья. Определим псевдополимино как набор полей, которые может обойти король. Как известно, король ходит на одно поле как по горизонтали или вертикали, так и по диагонали. Согласно определению, король, поставленный на любое поле псевдополимино, может достичь любого другого поля за конечное число ходов. Еще более общим является понятие квазиполимино, впервые введенное автором в статье "Шахматные доски и полимино" [7]. Квази-n-мино представляет собой произвольный набор n квадратов, которые можно мыслить себе как поля бесконечной шахматной доски.

Псевдополимино порядка n (или псевдо-n-мино), где n = 1, 2, 3 и 4, показаны на рис. 124. Из рис. 125, а видно, каким образом из пяти псевдотримино можно сложить прямоугольник размером 3×5. Из всех 22 псевдотетрамино, представленных на рис. 124, можно сложить лишь два прямоугольника: один размером 8×11, другой - размером 4×22. Оба эти прямоугольника можно составить из двух прямоугольников размером 4×11, сложенных из всех псевдотетрамино (см. рис. 125, б).

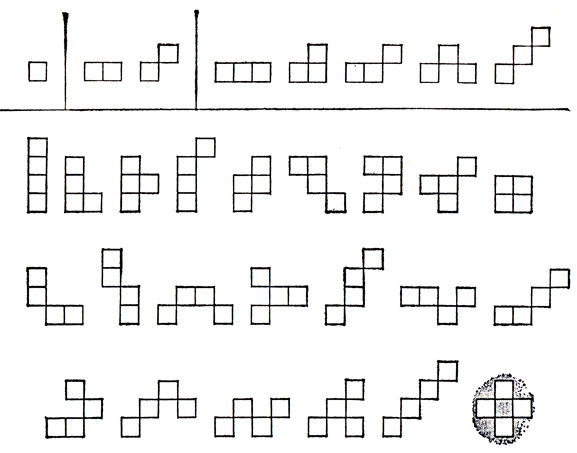
Рис. 124. Псевдо-n-мино для n = 1, 2, 3 и 4

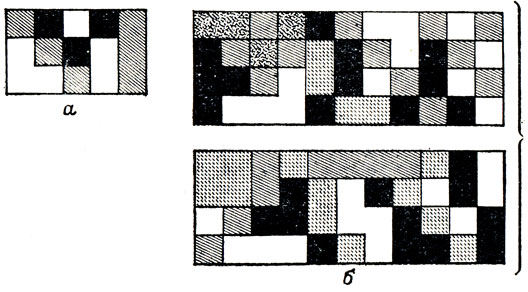
Рис. 125. Как построить прямоугольник из псевдополимино? а - 5 псевдотримино составляют прямоугольник 3×5; б - из 22 псевдотетрамино составлены два равных прямоугольника

Псевдополимино можно изучать не только на плоскости, но и в трехмерном или многомерном пространстве. Заметьте, что в обыкновенном (трехмерном) пространстве существуют три пространственных псевдодомино и 14 пространственных псевдотримино (не считая их зеркальных двойников); все они изображены на рис. 126. В отличие от обычных полимино число псевдо-n-мино неограниченно растет с увеличением размерности пространства, что заметно даже при малых n. Число разных псевдодомино в d-мерном пространстве в точности равно d (и поэтому на рис. 124 мы имеем два псевдодомино, а на рис. 126 - ровно три). Неизвестно, чему равно число всех псевдодомино в d-мерном пространстве: в случаях d = 1, 2 и 3 это число равно 1 + 4 + 9 + ... + d², однако никто не знает, верна ли соответствующая формула для следующих значений d.

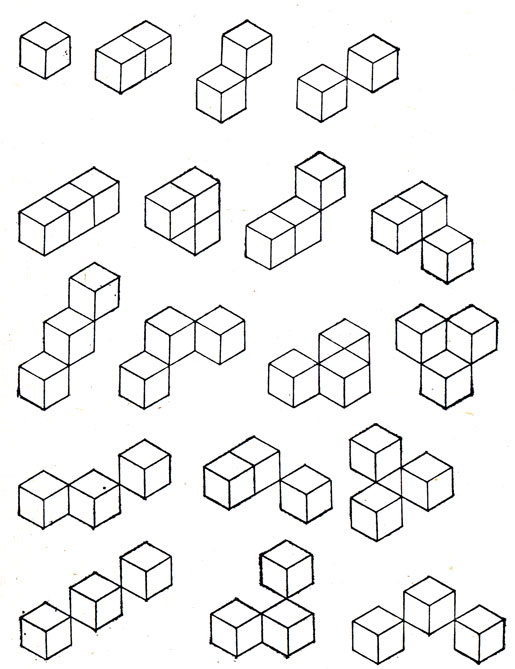
Рис. 126. Трехмерные псевдополимино

Рассмотренный выше метод порождения обычных (n + 1)-мино из n-мино с таким же успехом можно применить и к псевдополимино. А если несколько видоизменить условия, наложенные на размерности допустимых "строительных ячеек", то с его помощью можно одновременно найти и обычные полимино и псевдополимино. Именно с помощью этого метода были получены фигуры, изображенные на рис. 124 и 126. Можно также использовать технику подсчета раскрашенных или нераскрашенных деревьев, описанную в гл. VI, введя соответствующие правила.

Тематика, связанная с квазиполимино, имеет свою специфику. Сошлемся, в частности, на следующий пример: мы не в состоянии привести рисунки, изображающие все квазиполимино даже простейших типов, поскольку одних одномерных квазидомино существует бесконечно много. Поэтому для этой темы более типичны проблемы существования и вопросы о возможности построения интересующих нас фигур, в то время как для рассматриваемой ранее тематики характерны задачи, сводящиеся к непосредственному построению и к перечислению тех или иных конфигураций.

Одна из задач составления фигур из квазитримино приведена в уже упомянутой статье "Шахматные доски и полимино". В ней требуется найти покрытие обычной щахматной доски размером 8×8 с помощью 21 квазитримино типа изображенного на рис. 127, а и одного мономино. В решении, представленном на рис. 127, в, используются гексамино, составленные из двух таких квазитримино. Такое гексамино изображено на рис. 127, б.

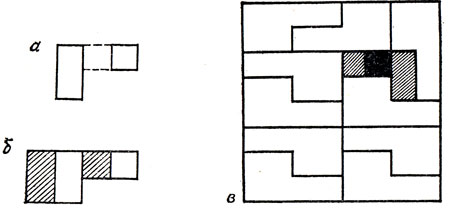
Рис. 127. Покрытие шахматной доски одним мономино и квазитримино

Бэзил Гордон, профессор математики Калифорнийского университета в Лос-Анджелесе, исследовал квазиполимино с целью получения ответа на следующий вопрос: каковы d-мерные квази-n-мино (где n должно быть возможно меньше), такие, что ими нельзя полностью замостить d-мерное пространство?

Гордон решил эту задачу для d = 1, когда "пространство" представляет собой просто прямую линию, разделенную на равные отрезки (рис. 128). В этом случае существует лишь одно квазимономино, которое представляет собой один такой отрезок (рис. 129, а), и ясно, как заполнить всю прямую такими отрезками.

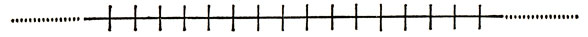
Рис. 128. Разбиение бесконечной прямой на равные отрезки

Любое одномерное квазидомино на нашей прямой состоит из двух отрезков и задается указанием расстояния t между этими отрезками, где t может быть равно 0, 1,2, 3, 4... (см. рис. 129, б). Очевидно, что t+1 таких фигур можно приложить одна к другой таким образом, чтобы ими покрылся отрезок длины 2t + 2. Подобное соединение показано на рис. 129, в, где одними номерами (от 0 до t) помечены компоненты квазидомино. Далее весьма просто заполнить полученными отрезками длины 2t + 2 всю изображенную на рис. 128 прямую.

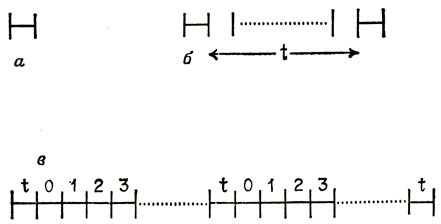
Рис. 129. Покрытие прямой квазидомино

Что же касается квазитримино, то, если запретить их переворачивать (то есть симметрично отображать), показанными на рис. 130 квазитримино нельзя покрыть всю прямую, ибо промежуток между двумя секциями фигуры заполнить нечем. В более интересном случае, когда разрешается переворачивать фигуру (то есть в случае двусторонних одномерных квазиполимино), Гордону удалось доказать следующую замечательную теорему: квазитримино каждого возможного типа можно полностью покрыть прямую. Например, два симметричных квазитримино типа изображенного на рис. 130 можно расположить так, что единичная секция одного войдет в промежуток между секциями другого; при этом окажется покрытым отрезок длины 6, повторения которого замостят всю прямую. Однако на рис. 131 представлены квазитетрамино, очевидным образом не покрывающие прямой. Следовательно, результат Гордона сводится к тому, что в одномерном случае каждое квазитримино (но не каждое квазитетрамино!) может покрыть бесконечную прямую.

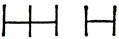
Рис. 130. Этими элементами нельзя покрыть прямую, если вращения запрещены

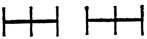
Рис. 131. Квазитетрамино, которыми нельзя покрыть прямую

Рассматривая случаи плоскости или пространства (трех или более измерений), Гордон указал квазиполимино из 3d ячеек (где d - размерность пространства), которое нельзя использовать для покрытия или, лучше сказать, "заполнения" пространства. Его идея иллюстрируется двумя примерами, приведенными на рис. 132, где d = 2 и 3. (В действительности в этих примерах фигурируют даже не квази-, а псевдополимино.) Эти примеры получаются следующим образом: прежде всего к пустой ячейке присоединяются все ее двумерные соседи, связанные с ней ходами ладьи. Кроме того, добавляются еще d ячеек, связанных с исходной пустой уже ходом короля. (Каждая из них связана с двумя уже добавленными ранее ходом ладьи.) Построение ячейки полностью изолирует первоначальную пустую. (Заметим, что это построение невыполнимо в одномерном пространстве.) Хотя приведенным построением доказывается существование квазиполимино из 3d ячеек, которыми нельзя заполнить d-мерное пространство (при d > 1), это вовсе не значит, что любое квазиполимино из 3d - 1 или еще меньшего числа ячеек подходит для заполнения пространства. Достаточно трудно доказать даже, что любым и квазиполимино из d + 1 ячеек можно заполнить d-мерное пространство.

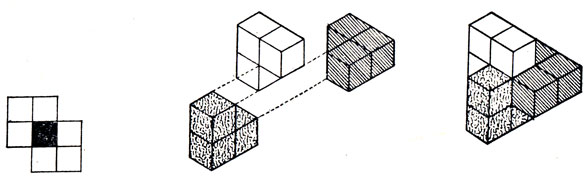
Рис. 132. Квазиполимино, которыми нельзя покрыть пространства

Специалист в области математической логики Э. Ф. Мур из "Бэлл телефон лабораториз" изучал задачи "заполнения" или покрытия d-мерного пространства неограниченным повторением конечного набора "стандартных" частей. Он высказал в высшей степени глубокое и интригующее предположение, относящееся ко всем задачам подобного рода и, в частности, к обсуждаемым нами задачам о заполнении пространства квазиполимино. Согласно этому предположению, какой бы конечный набор исходных частей ни подходил для того, чтобы, повторяя его элементы, можно было полностью заполнить d-мерное пространство, всегда существует некая ограниченная часть этого пространства, заполняемая элементами набора, такая, что все пространство можно покрыть неограниченным периодическим повторением этой части.

Высказанную Муром гипотезу подтверждает рис. 129, где из подходящим образом приложенных друг к другу квазидомино построен отрезок, повторными переносами которого можно покрыть всю бесконечную прямую. Мур не считает, что любое бесконечное покрытие (например, покрытие плоскости) обязательно является периодическим, то есть образованным периодическими повторениями одного и того же куска; такое утверждение, скорее всего, было бы неверным. Но он полагает, что если существует бесконечное покрытие какими-либо элементами, то существует и периодическое покрытие теми же элементами. По всей видимости, доказать или опровергнуть гипотезу Мура будет чрезвычайно трудно - ее автор даже одно время считал, что эта гипотеза относится к числу логически неразрешимых проблем. Однако недавно Муру и Ван Хао, профессору логики Гарвардского университета, кажется, удалось построить контрпример, в котором некоторое множество частей, покрывающих плоскость, нельзя преобразовать в периодическое покрытие плоскости.

Мы предлагаем читателю проверить, какими из 12 обычных и хорошо знакомых ему пентамино можно заполнить плоскость. Разумеется, плоскость должна быть заполнена однотипными пентамино. Следует различать случаи, когда покрытие плоскости можно произвести, не поворачивая пентамино, и случаи, когда поворот необходим. Пример покрытия, выполнимого только при условии возможности поворота, приведен на рис. 133.

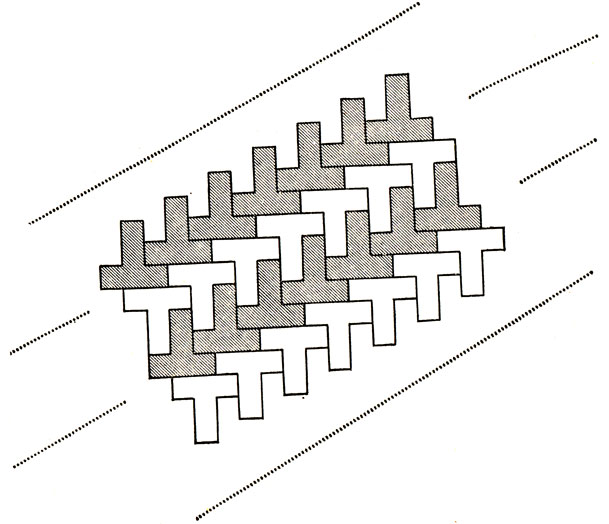
Рис. 133. Заполнение плоскости Т-пентамино