Приложение I.

Ответы к упражнениям гл. V

1. 8²×10⁵ = 6400000.

2. 12×15×9×13×11×12 = 2779920.

3. 26·25·24 - 1 = 15599.

4. 52·51·50·49·48·47 = 14658134400.

5. (₄⁶⁴) = 64·63·62·61 / 4·3·2·1 = 635 376.

6. (₈⁶⁴) = 64·63·62·61·60·59·58·57 / 8·7·6·5·4·3·2·1 = 4426165368.

7. (₆¹²) = 12·11·10·9·8·7 / 6·5·4·3·2·1 = 924.

8. (₃⁷) = 7·6·5 / 3·2·1 = 35.

9. (_5-1^4+5-1) = (₄⁸) = 70.

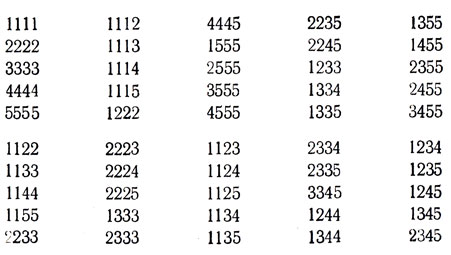
10. (_3-1^3+12-1) = (₂¹⁴) = 91.

11. Если считать все символы различными, то существует всего k! различных перестановок символов. При этом k₁ символов первого типа могут быть переставлены между собой k₁! способами, k₂ символов второго типа - k₂! способами и т. д., так что различных перестановок оказывается в k₁! k₂! ... k_r! раз меньше, то есть

12. Для слова окорок имеется 6! / 3! 2! 1! = 60 перестановок, а для слова Миссисипи 9! / 4! 3! 1! 1! = 10080 перестановок.

13.

14. Идея вывода формулы указана в "Указании". Непосредственный вывод мы предоставляем читателю.

15. Простые числа, меньшие 100, суть: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. Согласно нашей формуле:

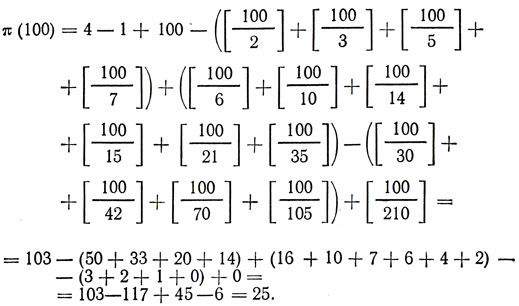
16. Здоровыми оказались 18 собак.

17. ¹/₂ (T + C)= ¹/₂ (1000 + 100) = 550.

18. ¹/₂ (Т + С) = ¹/₂ (26⁴ + 26²) = 228826.

19. Если k четное, N = ¹/₂ (n^k + n^k/2 ), если k нечетное, N = ¹/₂ (n^k + n^k+1/₂).

20. 32.

21. 28 обычных домино (от 0-0 до 6-6) и 55 "девятерных" (от 0-0 до 9-9).

22. 27 карточек занимают слишком много места, чтобы их можно было все здесь нарисовать.

23. N = ¹/₄ [n⁴ + 3/n²].

24. N = ¹/₄ (Т + С_а + С_b + С_с) = ¹/₄ (5⁶ + 5³ + 5³ + 5⁴) = 4125.

25. Н, I, О, X.

26. Если а и b нечетные, N = ¹/₄ (Т + С_а + С_b + С_с) = ¹/₄ (Т + С_а + С_b + С_c) = ¹/₄ (2^аb + 2^a(b+1/2) + 2^(a+1/2)b + 2^ab+1/2);

если а и b четные, N = ¹/₄ (Т + С_а + С_b + С_c) = ¹/₄ (2^аb + 2^ab/2) + 2^ab/2 + 2^ab/2) = ¹/₄ (2^ab + 3·2^ab/2);

если а нечетное, а b четное, N = ¹/₄ (Т + C_a + C_b + С_с) = ¹/₄ (2^ab + 2^ab/2 + 2^(a+1/2)b + 2^ab/2).

27. N = 1/4 (3⁴ + 2·3 + 3²) = 24.

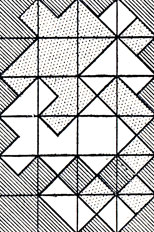
28. Как и раньше, 24. Мы приводим соответствующий чертеж.

29. N₄ = ¹/₄ (4⁴ + 2·4 + 4²) = 70.

N_n = ¹/₄ (n⁴ + 2n + n²) = ¹/₄ n (n + 1)(n² - n + 2).

Если n или n + 1 делятся на 4, то N_n очевидным образом - целое число. В любом случае одно из чисел n или n + 1 обязательно четное, а число n² - n + 2 всегда четное, так что произведение n(n + 1)(n² - n + 2) всегда делится на 4.

30. N₂ = ¹/₄ (2⁹ + 2·2³ + 2⁵) = 140.

31. N_n = ¹/₄ (n⁹ + 2·n³ + n⁵).

32. N_n = ¹/₄ (n^k2 + 2·n^1/₄k2 + n^1/₂k2) при четном k,

N_n = ¹/₄ (n^k2 + 2·n^{1/₄ (k2+3)} + n^{1/₂ (k2+1)} при нечетном k.

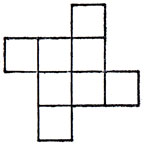
33. Октамино, переходящее в себя при повороте на 90 № (то есть обладающее поворотной симметрией четвертого порядка), изображено на рисунке.

N₂ = ¹/₄ (2⁸ + 2·2² + 2⁴) = 70.

34. N = ¹/₄ (n⁴ + 2·n + n²).

35. N = ¹/₈ (T + С₁₈₀ + 2С_H + 2С_D) = [¹/₈ (⁹₃) + 4 + 2·10 + 2·10] = 16.

Три мономино можно поставить на доску размером 3×3 следующими 16 способами (каждое мономино указано точками).

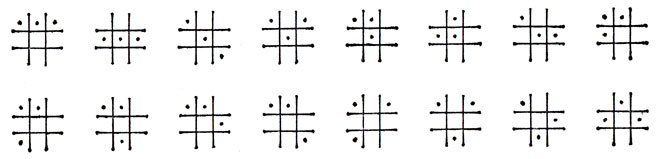
36. Для доски размером 4×4: N₄ = ¹/₈ (T + C₁₈₀ + 2C₉₀ + 2C_H + 2C_D) = ¹/₈ [(¹⁶₄) + (⁸₂) + 2·4 + 2·(⁸₂) + 2·(1 + 6·6 + 15)] = 252,

для доски размером 6×6: N₆ = ¹/₈ [(³⁶₄) + (¹⁸₂) + 2·9 + 2·(¹⁸₂) + 2[(⁶₄) + (⁶₂)(¹⁵₁) + (¹⁵₂)]] = 7509,

для доски размером 8×8: N₈ = ¹/₈ [(⁶⁴₄) + (³²₂) + 2·16 + 2·(³²₂) + 2[(⁸₄) + (⁸₂)(²⁸₁) + (²⁸₂)]] = 79920.

37. N = ¹/₈ (3¹⁶ + 3⁸ + 2·3⁴ + 2·3⁸ + 2·3¹⁰) = 5398083.

38. N = ¹/₈ [(⁹₅) + (⁴₂) + 2·2 + 2·12 + 2·12] = 23.

39. T = 3! (⁸₃)² = 18816.

N = ¹/₈ [18816 + 0 + 2·0 + 2·0 + 2·4 (⁸₃)] = 2408.

40. Для одного мономино N₁ = ⁿ²⁺²ⁿ/₈ при четном n, N₁ = ^n2+4n+3/₈ при нечетном n. Для двух мономино N₂ = ¹/₁₆ (n⁴ + 6n² - 4n) при четном n, N₂ = ¹/₁₆ (n⁴ + 8n² - 8n - 1) при нечетном n.

41. Х-пентамино имеет группу симметрии квадрата. I-пентамино имеет группу симметрии прямоугольника. Симметриями Т-, U-, V-, W- и Z-пентамино являются инволюции. F-, L-, N-, Р- и Y-пентамино обладают лишь тождественной (единичной) симметрией.

42. N₃ = ¹/₈ (3⁵ + 3³ + 2·3² + 2·3⁴ + 2·3³) = 63 раскрасок всего. N_abc = N₃ - 3N₂ + 3N₁ = 63 - 36 + 9 = 36 раскрасок, в которых встречаются всего три цвета.

43. Число расстановок ладей без учета симметрии T₄ = 4·3·2·1 = 24. Число расположений, не переходящих одно в другое при вращениях и зеркальных отражениях доски, равно N₄ = ¹/₈ (24 + 8 + 2·2 + 0 + 2·10) = 7.

44. Для шести ладей Т₆ = 6! = 720.

N₆ = ¹/₈ (720 + 6·4·2 + 0 + 0 + 2[1+ (⁶₄) + (⁶₂)·3 + 15]) = 115,

для восьми ладей Т₈ = 8! =40320.

N₈ = ¹/₈ (8! + (8·6·4·3·2) + 2·8 + 0 + 2[1+ (⁸₆)·1 + (⁸₄)·3·1 + (⁸₂)·5·3·1 + (⁸₀)·7·5·3·1]) = 5281.

45. N = ¹/₆ (2⁶ + 2 + 2² + 2³ + 2² + 2) = 14.

46. N = ¹/₁₂ (2⁶ + 2 + 2² + 2³ + 2² + 2 + 3·2⁴ + 3·2³) = 13.

47. Если допустимы лишь вращения, то для k цветов N = ¹/₆ (k⁶ + k³ + 2k² + 2k). Если же допустимы и вращения, и зеркальные отражения, то для k цветов

N = ¹/₁₂ (k⁶ + k³ + 2k² + 2k + 3k⁴ + 3k³) = ¹/₁₂ (k⁶ + 3k⁴ + 4k³ + 2k² + 2k).

В частности, при одних вращениях N₃ = 130 и N₄ = 700, а при вращениях и отражениях N₃ = 92 и N₄ = 430.

48. N = ¹/₆ (5³ + 2·5 + 3·5²) = 35.

49. Число различных ожерелий равно b^p. Для ожерелий с циклической группой симметрии N = ¹/_p [b^р + (р - 1) b], с диэдральной группой симметрий

N = ¹/_2p [b^p + (p - 1) b + pb^p+1/2]

Для b = 2 и р = 5 оба перечисления приводят к ответу 8. При b = 4 и р = 3 соответственные числа равны 24 и 20.

50. Всего 24 симметрии: одна тождественная; шесть поворотных, связанных вращениями на 90° относительно оси "от грани к грани" (поворотные симметрии четвертого порядка); три поворотных, связанных с вращениями на 180° относительно оси "от грани к грани" (поворотные симметрии второго порядка); шесть поворотных, связанных вращениями на 180° относительно осей "от ребра к ребру", и, наконец, восемь поворотных, связанных с вращениями на ± 120° относительно осей "от вершины к вершине" (поворотные симметрии третьего порядка).

51. N = ¹/₂₄ (6! + 0 + 0 + 0 + 0) = 30.

52. N = 2.

53. N = 6.

54. Если каждая из вершин либо остается на месте, либо отсекается, то

N = ¹/₂₄ (2⁸ + 6·2² + 3·2⁴ + 6·2⁴ + 8·2⁴) = 23.

Если же отсечены ровно четыре вершины, то

N = ¹/₂₄ [(⁸₄) + 6·2 + 3·6 + 6·6 + 8·2²] = 7.