Пространственное полимино

Многочисленные любители пентамино давно уже обнаружили возможность образования фигур не из пяти квадратов, а из пяти кубов. Из этих заготовок можно составлять различные пространственные тела. Не обязательно, конечно, ограничиваться числом 5: в принципе можно выписать и пересчитать пространственные полимино с любым заданным числом элементов. На рис. 112 показаны все пространственные полимино вплоть до тетрамино (где полимино задаются с точностью до положения в пространстве^*).

^* (Таким образом, полимино мы считаем одинаковыми, если их можно совместить (пространственным) движением, то есть переносом и поворотом вокруг оси.)

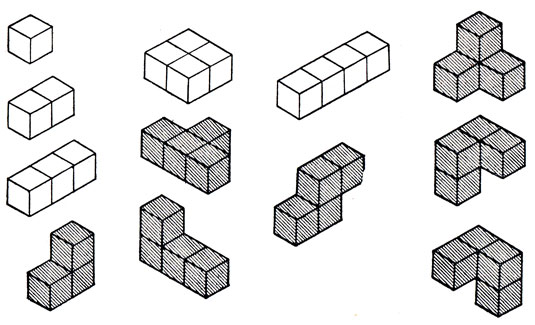
Рис. 112. Пространственные полимино низших порядков (заштрихованы кубики Сома)

Заметим, что первую существенно пространственную фигуру (то есть такую, что все образующие ее кубы нельзя "поставить" на одну плоскость) мы найдем лишь среди тетрамино. Это связано с тем обстоятельством, что любые три точки (скажем, центры кубов) всегда принадлежат одной плоскости, тогда как для четырех точек это не обязательно. Два из трех пространственных тетрамино "зеркально равны" друг другу, то есть их можно рассматривать как получающиеся зеркальным отображением друг друга, - они отличаются один от другого, как левый ботинок от правого, которые "почти одинаковы", но не могут быть совмещены друг с другом. Датчанин Пит Хейн, известный современный изобретатель игр и специалист по головоломкам, придумал игру, которую назвал "Кубики Сома". Кубики Сома представляют собой семь заштрихованных на рис. 112 пространственных тел: шесть тетрамино и одно тримино. Суть игры сводится к тому, чтобы сложить из перечисленных тел куб размером 3×3×3, а также множество других пространственных фигур, нередко весьма занимательных^*.

^* (Подробнее об этом читатель может прочесть в книге М. Гарднера [34].)

Если использовать пространственные аналоги 12 обычных пентамино, то естественно возникает задача о том, чтобы сложить из них прямоугольный параллелепипед размером 3×4×5. Одно из многих решений этой задачи последовательно показано на рис. 113.

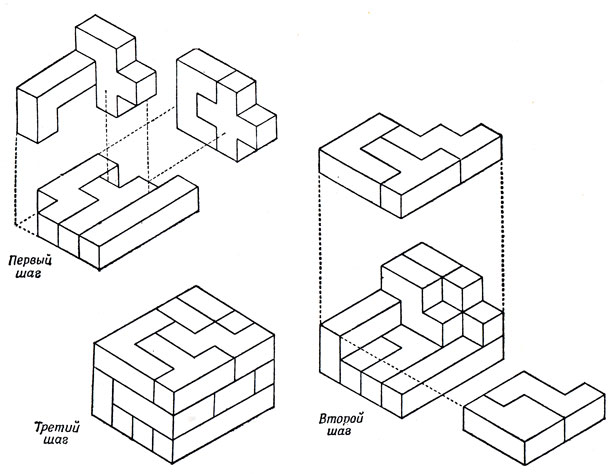
Рис. 113. Построение прямоугольного параллелепипеда 3×4×5 из двенадцати пространственных пентамино

Кроме упомянутого тела, из пространственных пентамино можно сложить также параллелепипеды размерами 2×3×10 и 2×5×6. Частное решение последней задачи, по сути дела, уже рассматривалось в гл. II при обсуждении первой задачи о "наложении", когда требовалось сложить из всех 12 пентамино два прямоугольника размером 5×6.

Дэвид А. Клэрнер рассмотрел все пространственные пентамино (он назвал их "пентакубиками"). Таких разных пентакубиков, из которых никакие два нельзя совместить движением в трехмерном пространстве, оказалось всего 29. "Зеркальные двойники", подобные изображенным на рис. 114, должны считаться различными, поскольку их можно перевести один в другой зеркальной симметрией - но не движением в пространстве. К сожалению, так как 29 - простое число, то из всех 29 пентакубиков нельзя сложить много простых тел. Но, как обнаружил Клэрнер, если отбросить "простейший" пентакубик - параллелепипед размером 1×1×5, то из оставшихся 28 можно составить два отдельных параллелепипеда размером 2×5×7. Решение Клэрнера приведено на рис. 115 (точками и крестиками отмечены места, в которых выступающие кубики - точки - входят в свободные ячейки - крестики). Другое решение, принадлежащее автору этой книги, показано на рис. 116. Его особенность заключается в том, что все 11 "плоских" пентакубиков (напомним, что пентакубик размером 1×1×5 исключен) включены в один из прямоугольных параллелепипедов размером 2×5×7.

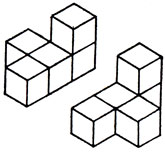
Рис 114. Зеркально симметричные пространственные пентамино

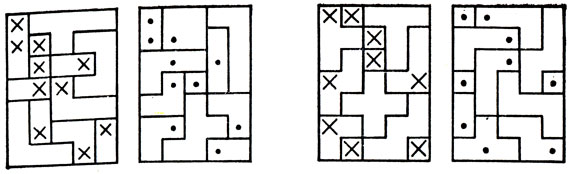
Рис. 115. Построение двух параллелепипедов 2×5×7 из пространственных пентамино

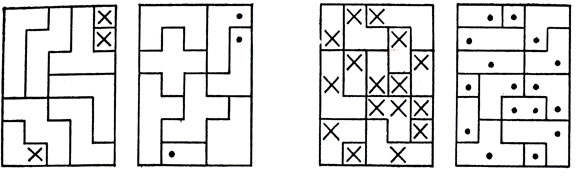
Рис. 116. 'Плоские' пространственные пентамино расположены лишь в одном из двух тел 2×5×7

Тех, кого заинтересует рассматриваемая проблема, приглашаем попробовать отыскать другие простые формы, составляемые из пространственных пентамино. Быть может, им удастся обнаружить другие, пока не известные формы соединения этих тел.