
Полимино высших порядков
Ниже систематизированы известные данные о числе n-мино как функции от n. (Достоверных сведений о числе n-мино, где n > 10, в литературе пока нет.)
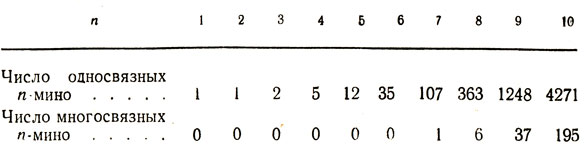
(Многосвязными называются полимино, содержащие пустоты внутри. Так, например, октамино, состоящее из восьми полей, которые окружают не принадлежащий октамино квадрат, будет многосвязным.)
Данные для n = 9 и 10 взяты из недавней статьи [24] Р. С. Рида, профессора математики Вест-Индского универг ситета в Кингстоне (Ямайка) В этой статье были разработаны методы подсчета числа n-мино, которые можно расположить в прямоугольниках размерами 1×р, 2×р, 3×р и т. д. (Здесь р - любое натуральное число.) В результате вычислений Рида оказалось, что существует ровно 1285 нонамино (состоящих из девяти квадратов) и 4466 декамино (из десяти квадратов); эти числа являются суммами столбцов приведенной справа таблицы. Метод Рида позволяет найти лишь суммарное число n-мино, а не число односвязных и многосвязных фигур в отдельности. Поэтому, чтобы согласовать данные двух последних таблиц, необходимо сложить число односвязных и многосвязных n-мино: 1248 + 37 = 1285; 4271 + 195 = 4466.
Независимо подобное же перечисление выполнил математик Томас Р. Паркин из компании "Аэроспейс корпорейшн" (Калифорния). Его данные во всем сходятся с опубликованными Ридом, за исключением числа декамино, помещающихся в квадрате размером 5×5. Здесь Паркин насчитал 529 декамино в отличие от 340 у Рида. До сих пор неизвестно, кто из них прав, поскольку пока никто не провел независимой проверки.
С методом перечисления Рида совершенно не связан другой способ подсчета, позволяющий непосредственно найти все n + 1-мино, если все n-мино нам известны. Для того чтобы пояснить этот способ, мы проиллюстрируем его на примере случая n = 4.
Для начала расположим все полимино n-го порядка по степени убывания длины наибольшего содержащегося в n-мино отрезка, состоящего из квадратов. Первый столбец рис. 105 изображает такое упорядочение тетрамино. Если n-мино обладает той или иной симметрией, то пометим крестиками внешние стороны образующих n-мино квадратов, симметричные сторонам какой-то выбранной "типичной области" (см. второй столбец рис. 105, где, например, в четвертой строке учитывается "поворотная симметрия", которой обладает соответствующее тетрамино). Теперь к любой свободной (то есть не помеченной крестиком) стороне добавим внешний квадрат. Начнем с самого "длинного" n-мино, получая новые (n + 1-мино для случая тетрамино, изображенные в третьем столбце рис. 105. Переходя затем к более "коротким" n -мино, необходимо предусмотреть возможность "порождения" из них уже найденных нами ранее фигур. Однако, чтобы избежать повторений, нам достаточно просто ограничить крестиками "длину" наибольшего отрезка, как это показано в четвертом столбце рис. 105. Первое из двух приведенных там тетрамино, будучи дополнено еще одним полем, присоединенным к свободному ребру, порождает целую последовательность пентамино, представленную на рис. 106. Предупредим возможность получения этих же фигур из других n-мино той же "длины" (рис. 107, а), после чего последовательно применим к ним процесс порождения, в нашем случае приводящий к единственной фигуре, изображенной на рис. 107, б.
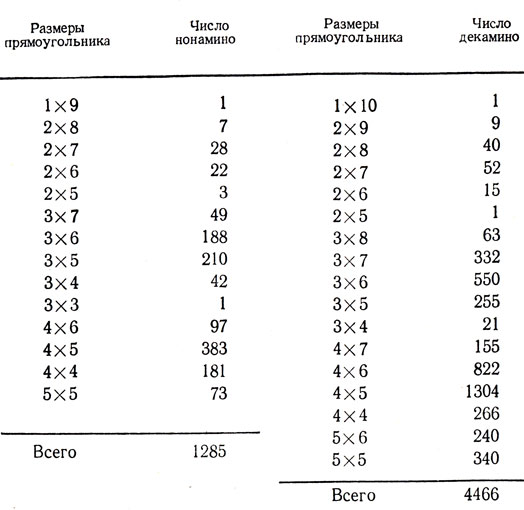
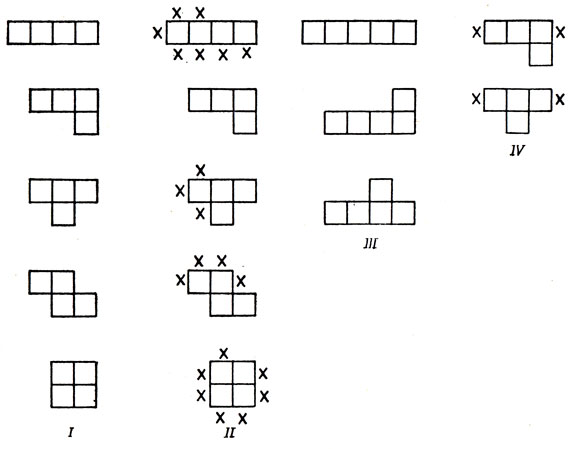
Рис. 105. Порождение пентамино из тетрамино

Рис. 106. Пентамино, порожденные из первого тетрамино четвертого столбца на рис. 105
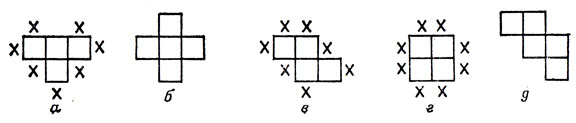
Рис. 107. Найдены два последних пентамино
Исчерпав все возможности с n-мино "второй длины", перейдем к n-мино следующей "длины". И в этом случае надо прежде всего запретить порождение отрезков "второй длины" (рис. 107, в и г), после чего повторим всю процедуру. В итоге получим пентамино, показанное на рис. 107, д.
Продолжая действовать тем же способом, мы, исходя из имеющихся n-мино, породим все (n + 1)-мино, причем каждая из последних возникнет у нас лишь один раз. (Так, в нашем примере мы действительно получили все 12 пентамино.) Этот способ, который в общем случае требует некоторого усовершенствования, весьма подходит для реализации его на электронной вычислительной машине, ибо он одновременно обладает как однозначностью, так и систематичностью - двумя качествами, присущими реализуемым на ЭВМ вычислительным процессам. Надо лишь отметить что единственность порождения (n + 1)-мино из некоторых n-мино обеспечивается введением еще одного ограничения. Для того чтобы пояснить, что мы имеем в виду, рассмотрим еще один пример.
Пусть n = 5 и в качестве первого элемента "третьей длины" взято Р-пентамино, не обладающее никакой симметрией. Тогда запрещающие крестики будут поставлены так, как на рис. 108, слева. Если теперь к этой фигуре применить нашу процедуру, мы придем к семи гексамино, показанным на рис. 108, а-ж. Нетрудно, однако, заметить, что фигуры в и е совпадают, так что, с учетом их обеих, мы сделаем ошибку в перечислении. Удвоение требуемого результата связано здесь с тем, что одна из указанных фигур получается из другой поворотной симметрией (проще сказать, вращением на 90°). Чтобы понять, почему возникает удвоение, изучим сначала полимино, обладающие "поворотной симметрией четвертого порядка", то есть переходящие в себя при повороте на 90°, - некоторые из них изображены на рис. 109. Если какое-либо полимино получается из одной из этих фигур добавлением к ней одного или двух мономино, "расположенных под углом 90°", то мы можем встретиться с той же трудностью, что и в случае Р-пентамино. Впрочем, если фигура, порожденная таким образом из обладающего "поворотной симметрией четвертого порядка" полимино, сама симметрична (причем непременно симметрична относительно некоторой оси), то опасности не возникает (то есть удвоения не произойдет). На рис. 110 показаны формы, которые возникают из изображенных на рис. 109 полимино путем добавления одного или двух квадратов, "расположенных под углом 90°". Особого внимания здесь заслуживают лишь не обладающие симметрией фигуры, затененные на нашем рисунке.

Рис. 108. Гексамино, порожденные Р-пентамино
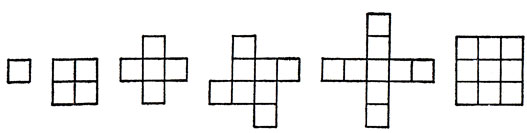
Рис. 109. Полимино, инвариантные относительно поворота на 90°
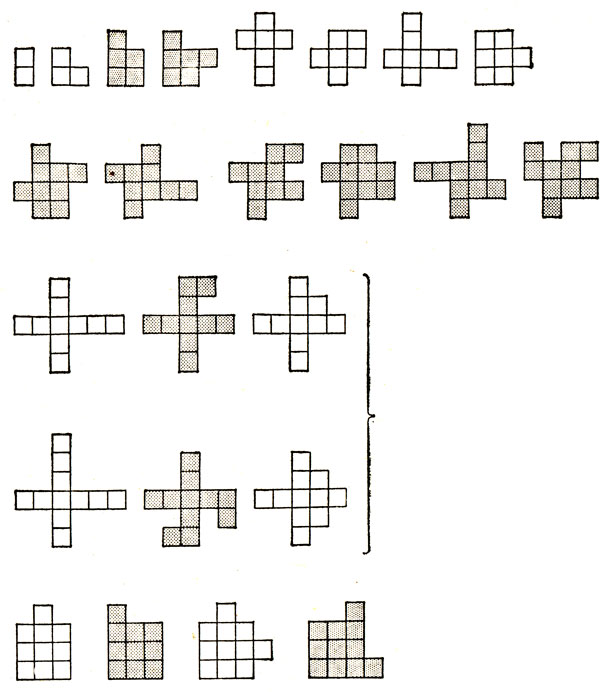
Рис. 110. Полимино высших порядков, полученные из фигур на рис. 109
По сравнению с тысячами полимино, для которых n < 13, эти 12 особых фигур представляют редчайшее исключение. Поэтому при составлении программы для ЭВМ или в процессе любого другого аналогичного подсчета удвоением числа этих фигур можно пренебречь, отложив работу по исключению "лишних" фигур до составления полного списка всех (n + 1)-мино, получаемых нашей процедурой из n-мино.
Известно, что существует 369 октамино, включая шесть многосвязных фигур, право на включение которых в список всех октамино может вызывать известное сомнение. Эти "дырявые" октамино изображены на рис. 111, где указано отверстие внутри фигуры. Все они порождаются многосвязным гептамино, заштрихованным на рис. 103.

Рис. 111. Многосвязные октамино
Точное выражение зависимости числа Р(n) всех различных n-мино от n еще не найдено. Эмпирически определен ряд значений отношения Сn, где
| Cn = | P(n+1) | , |
| n P(n) |
а именно найдено, что С1 = 1, С2 = 1, С3 = 0,833, С4 = 0,600, С5 = 0,583, С6 = 0,514, С7 = 0,488, С8 = 0,435, С9 = 0,386. Возможно, что эта последовательность имеет предел. Если этот так, то
P(n) ≈ k·Cn·n!,
где C = limn→∞ Cn (а Cn - просто (C)n).
Во всяком случае, нетрудно доказать, что
P(n + 1) < (2n + 1) P(n).
Действительно, простое наблюдение показывает, что, за исключением "прямого" n-мино, к любому другому внешний квадрат можно добавить самое большее 2n + 1 способами. С учетом же соображений симметрии легко установить, что существует всего n + 3 / 2 (что, конечно, меньше чем 2n + 1) вариантов добавления квадрата к прямому n-мино. Из последнего неравенства следует, что Р (n) < (2n)! / 2n n! А поскольку в силу формулы Стерлинга правая часть этого неравенства растет как
| 1 | 2nn!, | |
| √πn |
то последнее выражение задает оценку сверху для Р(n). Конечно, полученное довольно простое выражение не является наилучшей оценкой, однако оно может послужить первым шагом в решении нашей задачи.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'