Гексамино и гептамино

Существует всего 35 различных (двусторонних) гексамино, общая площадь которых равна 210 единичным квадратам. Из них нельзя сложить никакого прямоугольника - ни прямоугольника размером 3×70, ни размером 5×42, 6×35, 7×30, 10×21 или 14×15. (Это было доказано в конце гл. I с помощью простых соображений, связанных с шахматной раскраской соответствующей прямоугольной "доски") Тем не менее, как было показано в одном из номеров недолго просуществовавшего английского журнала Fairy Chess Review, интересные укладки всех гексамино все же имеются. Две из них изображены на рис. 101 и 102.

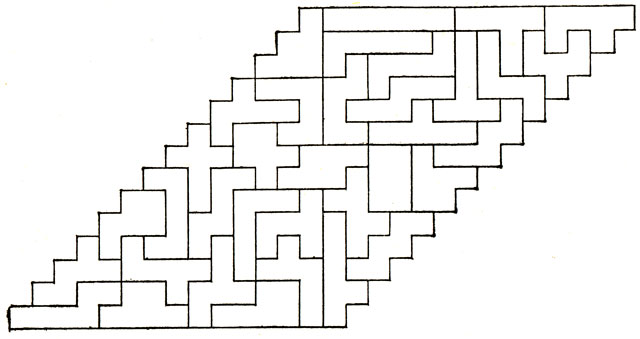
Рис. 101. Укладка гексамино

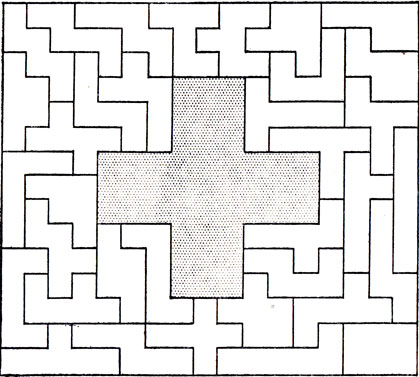
Рис. 102. Симметричная укладка гексамино

Существует ровно 108 разных (двусторонних) гептамино, причем в это число входит и одно "дырявое" гептамино (заштрихованное на рис. 103). Некоторые предпочитают исключать это гептамино из общего списка, поскольку любая содержащая его укладка будет иметь "дырку" и наши гептамино никак не смогут покрыть всю заполняемую ими фигуру. Общая площадь остальных 107 гептамино, очевидно, равна 7×107 = 749 квадратных единиц. Единственный прямоугольник, который могли бы заполнить все эти гептамино, - это прямоугольник размером 7×107. (Разумеется, не может быть и речи о покрытии этими гептамино прямоугольника размером 1×749.) Весьма интересную укладку, показанную на рис. 104, нашел Дэвид А. Клэрнер из Гумбольдтского городского колледжа в Калифорнии - здесь все 107 гептамино образуют один квадрат размером 7×7 и четыре прямоугольника размером 7×25. Читатель может попробовать найти другие варианты укладки 107 "односвязных"^* гептамино. Клэрнер же первым решил и задачу об укладке всех 108 гептамино в три прямоугольника размером 11×23 с отверстием в центре каждого из них. Это решение Клэрнера показано на рис. 103.

^* (То есть не имеющих отверстий.)

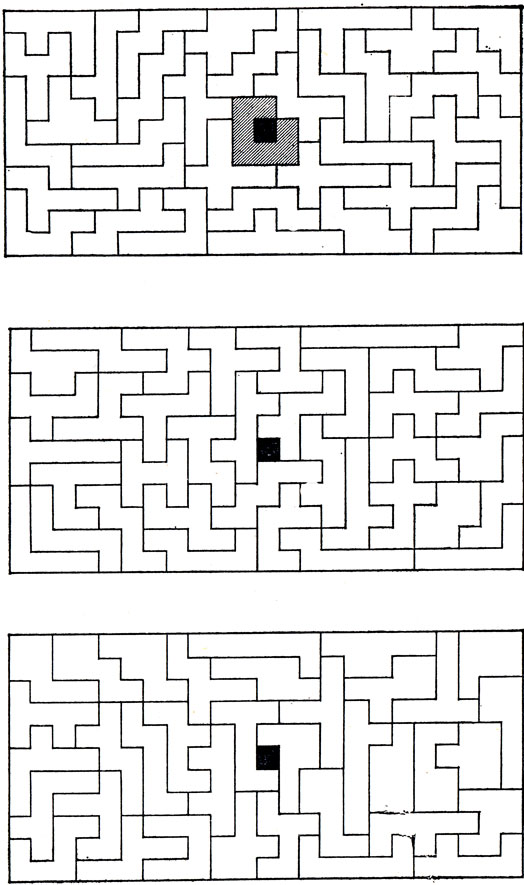
Рис. 103. Три равных прямоугольника, покрытые 108 гептамино

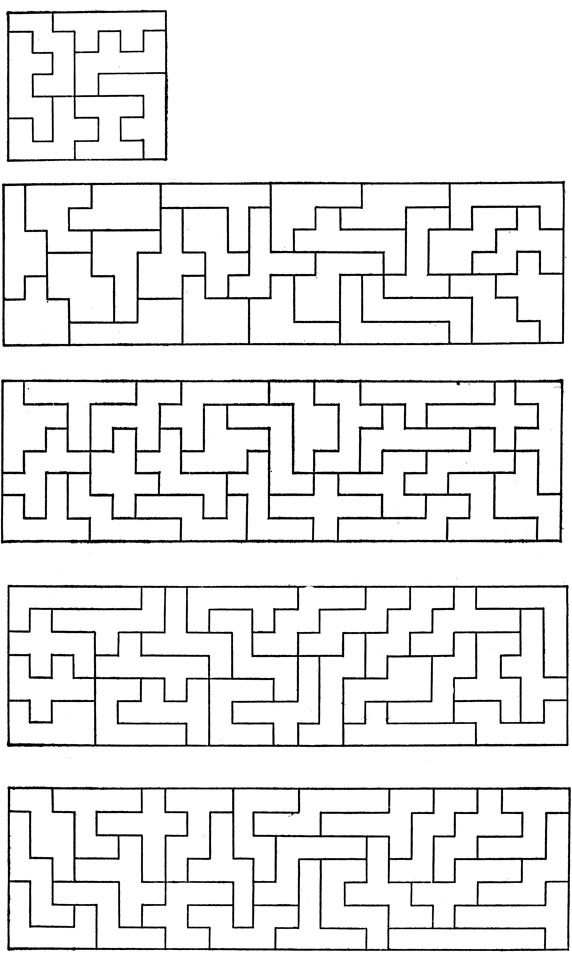
Рис. 104. Четыре прямоугольника и квадрат, покрытые 107 гептамино