Односторонние полимино

До сих пор мы допускали, что при укладке полимино их можно как поворачивать, так и переворачивать, то есть зеркально отображать. Однако если запретить извлечение геометрических фигур из той плоскости, в которой они лежат, то мы по-прежнему сможем вращать фигуры, но не сможем уже их зеркально отображать. Полимино, которые запрещено переворачивать, естественно называть односторонними. Понятно, что односторонних n-мино должно быть больше, чем обычных "двусторонних". Так, хотя по-прежнему существует лишь одно одностороннее мономино, одностороннее домино и два односторонних тримино, уже различных односторонних тетрамино становится семь (вместо пяти), односторонних пентамино - 18 (вместо 12), односторонних гексамино - 60 (вместо 35) и т. д. Как и пять двусторонних тетрамино, семь односторонних тетрамино нельзя уложить в прямоугольник. На рис. 99 показано, как можно уложить все односторонние тетрамино в связную (и даже в симметричную) фигуру. На рис. 100 изображен прямоугольник размером 9×10, сложенный из всех 18 односторонних пентамино. (Доля тех n-мино, которые не тождественны своему зеркальному отражению, с ростом n стремится к 1.) Ниже нас будет интересовать в основном случай двусторонних полимино, но иногда мы будем говорить и об односторонних, различая зеркально симметричные полимино.

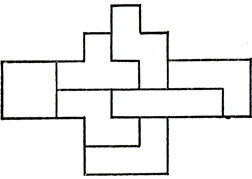
Рис. 99. Почти симметричная укладка односторонних тетрамино

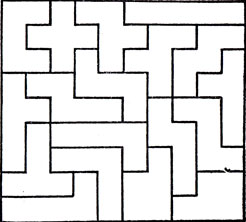
Рис. 100. 18 односторонних пентамино составляют прямоугольник