Многомерные пентамино и прямоугольные деревья

Выписать все n-мино, которые можно образовать в пространстве неограниченного числа измерений^* (по крайней мере, для небольших значений n), не так трудно, как можно было бы вообразить. Легко заметить, что любое n-мино (образованное из n связанных ячеек или "гиперкубиков") по существу всегда можно вместить в пространство не более чем n-1 измерений (которое можно "натянуть" на n центров ячеек). Поэтому лишь начиная с пентамино мы можем рассчитывать на возможность выхода за пределы трехмерного пространства.

^* (По поводу понятия многомерного пространства (и многогранников в этих пространствах) см., например, Б. А. Розенфельд, И. М. Яглом, Многомерные пространства, Энциклопедия элементарной математики, кн. V (геометрия), М., изд-во "Наука", 1966, стр. 349-392.)

Особенно проста конструкция тех n-мино, для расположения которых необходимо иметь пространство максимально возможной размерности n-1. Заметим, что, поскольку мы не налагаем ограничений на размерность пространства, "зеркальные двойники" не следует считать различными: они переводимы один в другой движением в пространстве большей размерности, подобно тому как односторонние пентамино, которые в плоскости приходится считать различными, могут быть совмещены, если при перемещении в трехмерном пространстве разрешается выводить их из плоскости.

Для целей представления наших тел удобно заменить каждую ячейку конструкции (квадрат, куб, гиперкуб) единственной точкой - центром данной ячейки - и соединить отрезками прямых центры соседних ячеек. Так, изображенное на рис. 117, а тетрамино перейдет в воспроизведенное на рис. 117, б "дерево"^*. Математики в таких случаях говорят, что дерево проективно двойственно тетрамино.

^* (По поводу деревьев и других графов см., например, элементарную книгу: О. Оре, Графы и их применение, М., изд-во "Мир", 1965, или более серьезную монографию Ф. Харари [47^*].)

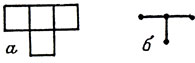
Рис. 117. Представление тетрамино в виде 'дерева'

Для того чтобы учитывать многомерные конструкции, условимся в рассматриваемых схемах отмечать расположенные в пространствах отрезки разных размерностей по-разному (с линиями, точками, пунктиром и т. д.). На рис. 118 в соответствии с этим допущением показаны схемы различных мономино, домино, тримино, тетрамино и пентамино. При этом горизонтально расположенным отрезкам (это направление мы считаем отвечающим первой размерности) соответствуют сплошные линии, вертикально расположенным отрезкам (вторая размерность) - пунктирные, отрезкам, перпендикулярным плоскости листа книги (третья размерность) - линии из точек, а отрезкам четвертой размерности - штрихпунктирные линии.

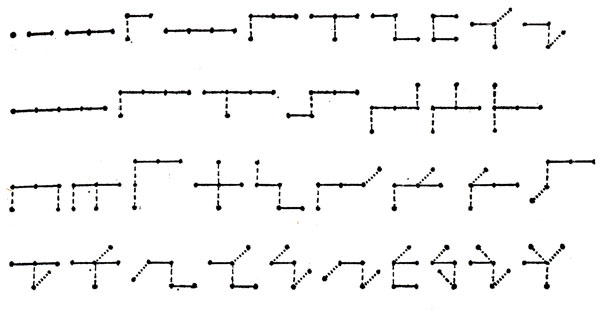
Рис. 118. Все полимино до пентамино в пространстве неограниченной размерности

На рис. 118 мы находим лишь семь тетрамино, тогда как на рис. 112 их было восемь. Это объясняется тем, что последние два тетрамино на рис. 112 являются зеркальными двойниками. Подобным же образом вместо 29 пентамино, найденных Клэрнером, мы обнаруживаем всего 23 пентамино в одно-, двух- и трехмерном пространствах, так как среди "пентакубиков" Клэрнера имеются шесть пар зеркальных двойников. Последние три пентамино на рис. 118 располагаются только в четырехмерном пространстве.

Вопросу перечисления многомерных деревьев посвящена обширная математическая литература. Весьма обстоятельно изложен этот вопрос в шестой главе упомянутой выше книги Дж. Риордана [41]. Нашим целям благоприятствует то обстоятельство, что перечисление "прямоугольных" деревьев типа изображенных на рис. 118 может быть выполнено уже разработанными в науке методами. Для их применения достаточно отождествить "прямоугольное" дерево с деревом (то есть множеством точек, соединенных линиями так, что из каждой точки в каждую ведет единственный путь), "ребра" которого (то есть дуги, соединяющие точки, называемые "вершинами" дерева) "раскрашены" по-разному. Обыкновенные "нераскрашенные" деревья до шестого порядка показаны на рис. 119 (дерево "шестого порядка" имеет шесть вершин и пять соединяющих их ребер).

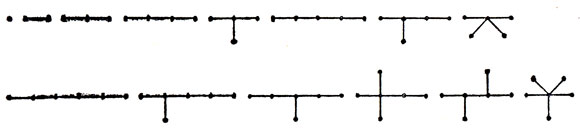
Рис. 119. Обычные 'деревья' до шестого порядка

Для того чтобы установить эквивалентность между полимино и "раскрашенными" деревьями, следует помнить некоторые правила, касающиеся раскраски деревьев:

1. Из любой вершины дерева не должно исходить более двух одноцветных ребер.

2. Деревья, отличающиеся лишь перестановкой (переименованием) цветов, следует считать одинаковыми.

3. Каждому ребру должно быть приписано "направление" (другими словами, либо знак "плюс", либо "минус").

Деревья с одинаковой раскраской и различной ориентацией считаются эквивалентными лишь тогда, когда можно добиться совпадения ориентации одновременным изменением знаков у каждого ребра одного цвета. (Ориентацию удобно указывать стрелкой у конца ребра.)

4. В любой линейной последовательности ребер дерева не разрешается иметь одинаковое число противоположно ориентированных ребер любого цвета. (Смысл этого правила заключается в том, что при переходе от деревьев к полимино отсеки не "возвращаются на занятые места".)

При выполнении перечисленных правил исходные деревья, изображенные на рис. 119, отождествляются с прямоугольными деревьями рис. 118, что и показано для мономино, домино, тримино, тетрамино на рис. 120.

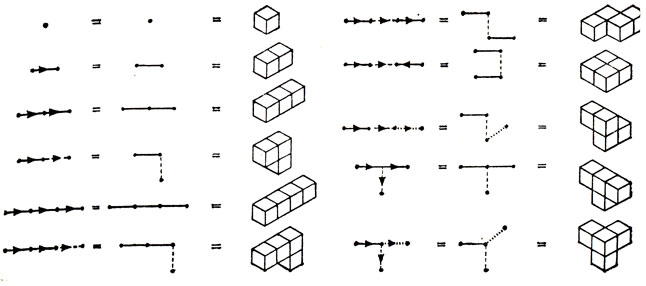
Рис. 120. Превращение 'деревьев' в полимино

К сожалению, для полимино высших порядков соответствие между полимино и прямоугольными деревьями нарушается. Трудность, с которой мы уже сталкивались, иллюстрируется рис. 121, на котором показаны четыре неэквивалентных дерева, каждое из которых "отвечает" одному Р-пентамино.

Рис. 121. Четыре неэквивалентных дерева, приводящие к одному Р-пентамино

Аналогичный характер имеет и рис. 122, на котором показаны два различных представления в виде дерева одного и того же пространственного пентамино. Правда, случаи множественности представлений в виде деревьев для пентамино этим исчерпываются. Но с возрастанием порядка полимино ситуация все более усложняется. Впрочем, возможно, имело бы смысл, не обращая внимания на возникающие здесь трудности, все же попытаться применить технику перечисления деревьев к определению числа возможных полимино. В этом случае, если бы нас интересовало число плоских полимино, необходимо бы было рассматривать дихроматические (двухцветные) деревья.

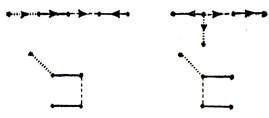
Рис. 122. Два различных дерева, отвечающие одному пространственному пентамино

Однако рассмотрения одного случая раскрашенных деревьев достаточно для исчерпывающего ответа на интересующий нас вопрос. Речь идет о случае n-мино, располагающихся лишь в пространстве максимальной размерности n-1. Деревья таких n-мино содержат по n вершин, соединенных n-1 ребрами, окрашенными в разные цвета. Это обстоятельство полностью устраняет все неприятности, связанные с симметрией и ориентацией. Поэтому для деревьев с n вершинами и n-1 ребрами существует единственное такое n-мино (правила, введенные применительно к этим деревьям, позволяют рассматривать просто нераскрашенные деревья). Следовательно, возвращаясь к рис. 119, мы находим, что существует одно одномерное домино, одно двумерное тримино, два трехмерных тетрамино, три четырехмерных пентамино и шесть пятимерных гексамино. Все они представлены на рис. 123, где жирной чертой обозначен пятый цвет.

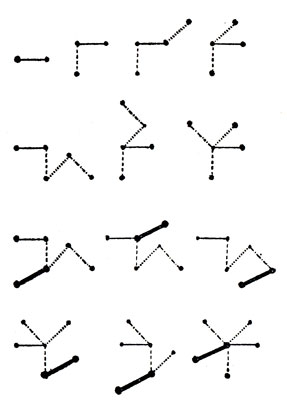
Рис. 123. n-мино, располагающиеся в (n - 1)-мерном пространстве