Включение и исключение

Известна старинная шутка о том, что лошадь имеет не меньше 12 ног: две спереди, две сзади, по две с каждого бока, по одной "с каждого угла" - и это не считая ног, которые снизу!

Аналогичный "парадокс" связан с доказательством того, что в течение года человек не успевает работать. Действительно, из 365 дней в году 104 падают на субботние и воскресные дни, 7 - на праздники, 10 - на отпуск^*. Далее, ¹/₃ времени, то есть 122 дня, уходит на сон, а другая треть, то есть еще 122 дня, лежит за пределами восьмичасового рабочего дня. Итак, 104 + 7 + 10 + 122 + 122 = 365 дней в году, не занятых работой!

^* (Здесь автор исходит из данных, относящихся к его стране; читатель может, разумеется, перевести их на наши условия - при этом окажется, что свободного времени в году у него свыше 365 дней!)

Очевидно, что "изюминка" рассмотренных выводов заключается в наличии пересечений различных групп, которые мы подсчитывали как якобы независимые. Так, спереди и с правого бока у лошади есть общая нога, а все "угловые" ноги одновременно находятся и снизу. Подобным же образом, часть восьмичасовых отрезков времени, отводимых для сна, приходится на выходные и праздничные дни; поэтому в приведенном выше решении они считались дважды. Существует весьма простая формула, дающая точный ответ на любую задачу подобного типа и учитывающая все пересечения суммируемых групп. Она носит название "формула включений и исключений" (иногда ее называют также формулой перекрестной классификации).

Теорема 6. Пусть задано множество, содержащее N элементов, причем N₁ из них обладают свойством Р₁, N₂ - свойством Р₂ и так далее, наконец, N_r обладают свойством Р_r. Тогда число элементов, которые не обладают ни одним из свойств Р₁, Р₂, ..., Р_r (обозначим это число через N₀) равно

где через N_i,j...m обозначено число элементов, обладающих одновременно свойствами Р_i, Р_j, ... , Р_m.

Пример. Возьмем N = 365, а через P₁ обозначим свойство дня быть выходным, Р₂ - праздником, Р₃ - днем отпуска, через Р₄ - свойство быть временем, потраченным на сон, и через Р₅ - нерабочее время, в течение которого человек бодрствует. Тогда N₁ = 104 дня, N₂ = 7 дней, N₃ = 10 дней, N₄ = N₅ = 122 дня. При этом N_1,4 = 104:3 = 34²/₃ дня; N_2,4 = 7:3 = 2¹/₃ дня; N_3,4 = 10:3 = 3¹/₃ дня; N_1,5 = 104:3 = 34²/₃ дня; N_2,5 = 7:3 = 2¹/₃ дня и, наконец, N_3,5 = 10:3 = 3¹/₃ дня. Остальные N_{i,j, ..., m} = 0. Следовательно, N₀ (рабочее время) равно N₀ = N - (N₁ + N₂ + N₃ + N₄ + N₅) + (N_1,4 + N_2,4 + N_3,4 + N_1,5 + N_2,5 + N_3,5) = 365 - 365 + ²⁴²/₃ = 80²/₃ дня = 1936 ч = 48,4 сорокачасовой рабочей недели.

Доказательство. Из исходного множества в N элементов мы вычитаем N₁ элементов, обладающих свойством Р₁, N₂ элементов, обладающих свойством Р₂, и т. д. Однако каждый элемент, обладающий двумя из этих свойств, вычитался дважды. Поэтому эти элементы следует восстановить, для чего необходимо добавить члены N_i,j. Далее, элементы, обладающие тремя из данных свойств - например, свойствами Р_i, P_j и P_k, - трижды вычитались (рассмотрите выражение - N_i - N_j - N_k) и трижды восстанавливались (рассмотрите сумму N_i,j + N_i,k + N_j,k). Поэтому их следует вычесть из N, что мы и делаем, добавляя члены - N_i,j,k. В общем случае элемент, обладающий t из наших r свойств, вычитался t раз, затем добавлялся (₂^t) раз, снова вычитался (₃^t) раз, добавлялся (₄^t) раз и т. д. В результате он был добавлен к N ровно - t + (₂^t) - (₃^t) + - ... ± (_t^t) раз. Это выражение на 1 меньше, чем 1 - (₁^t) + (₂^t) - (₃^t) + - ... ± (_t^t) = 0 (ср. свойство 2 биномиальных коэффициентов на стр. 90). Поэтому в итоге любой элемент, обладающий хотя бы одним из r указанных свойств, был вычтен из N ровно один раз^*.

^* (Более краткое (но также требующее известного внимания) доказательство формулы включений и исключений базируется на принципе математической индукции (ср. выше, стр. 19); оно приведено, например, в книге Н. Я. Виленкина, стр. 26-27 (см. сноску на стр. 80).)

1. Рыбак собирается ловить рыбу на площади 1000×1500 миль (рис. 91). Однако ему запрещено заходить в районы A, В и С, представляющие собой квадраты со сторонами 500 миль, центры которых удалены один от другого на 400 миль. На какой площади может он ловить рыбу?

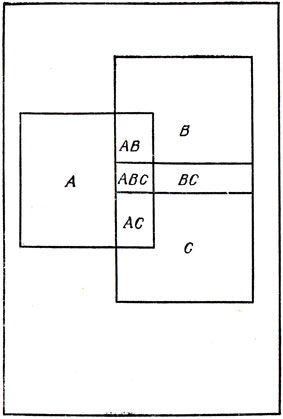
Рис. 91. Задача рыбака

Площадь ловли рыбы F получится из площади всего района Т вычитанием площадей А, В, С, затем добавлением площадей, принадлежащих одновременно А и В, А и С, В и С (каждая из них содержит площадь, принадлежащую всем трем районам), и, наконец, вычитанием общей площади трех районов А, В и С. Нахождение численного ответа оставляем читателю в качестве упражнения.

2. Пусть число n имеет различные простые делители р₁, р₂, ..., р_r. Сколько чисел от 1 до n взаимно просты с n (то есть не имеют с n общих простых делителей)?

Соответствующее число обозначается φ(n); эта функция от n называется функцией Эйлера. (По разным соображениям число 1 не рассматривается как простое. Если бы мы считали 1 простым числом, то для любого числа, меньшего п, нашелся бы общий с n простой делитель; поэтому для всех n мы имели бы φ(n) = 0.) Поэтому φ(1) = 1; φ(2) = 1; φ(3) = 2; φ(4) = 2; φ(5) = 4; φ(6) = 2; φ(7) = 6; φ(8) = 4 и т. д.

Обозначим через Р₁ свойство делиться на р₁, через Р₂ - свойство делиться на р₂, ..., через Р_r - свойство делиться на р_r. Тогда, по теореме 6,

13. Для каждого значения n от 1 до 15 выпишите числа, меньшие n и не имеющие с ним общих делителей. (Простые числа в промежутке от 1 до 15 суть 2, 3, 5, 7, 11, 13.) Сравните полученные вами списки с ответами, найденными из только что выведенной формулы

14. Пусть p₁, p₂, ..., p_m - простые числа, не превосходящие √x. Покажите, что число простых чисел, не превосходящих х (обозначаемое через π(х)), задается выражением

где через [x/p] обозначена так называемая целая часть дроби x/n, т. е. наибольшее целое число, не превосходящее x/p. (Указание: а) Если число между 1 и х - составное, то хотя бы один из его простых делителей будет меньше √x. Почему? б) Число кратных р чисел, не превосходящих x, равно [x/p]. Почему? в) Не забудьте включить в π(х) первые m простых чисел и исключить единицу, которая не является простым числом.)

15. Простые числа, не превосходящие √100, суть 2, 3, 5 и 7. Используйте формулу предыдущей задачи для нахождения π(100). Совпадает ли ответ с непосредственно подсчитанным числом простых чисел от 1 до 100?

16. Среди 50 бездомных собак 12 болеют чумкой, у 18 - блохи, у 11 - глисты и шесть собак бешеные. Кроме того, у пяти из них чумка и блохи; у трех собак - блохи и бешенство, у четырех - чумка и глисты, у пяти - блохи и глисты, а у двух - чумка, блохи и глисты одновременно. Предполагая, что эти собаки больше ничем не болеют и среди них нет собак, больных другими комбинациями болезней, определите, сколько среди этих 50 собак здоровых?