Подсчет разнородных объектов

Как узнать, сколько коров в стаде? Надо сосчитать, сколько у них ног, и разделить полученное число на четыре. А как узнать, сколько машин на стоянке? Опять-таки достаточно подсчитать, сколько у них колес, и разделить ответ на четыре! Если же на стоянке находятся не только автомобили, но и велосипеды и одноколесные тачки, то число экипажей, разумеется, не будет равно четверти числа колес. Истинное число экипажей Э можно получить с помощью формулы

где А обозначает число автомобильных колес, В - число колес велосипедов, а Т - число колес тачек. На самом деле, ¹/₄ A - число автомашин, ¹/₂ В - число велосипедов и Т - число тачек, так что наша формула представляет собой просто сумму этих чисел. Как мы увидим впоследствии, эта формула является частным случаем другой, гораздо более общей формулы подсчета, в которой соответствие между членами формулы и подсчитываемыми элементами будет не столь простым.

Предположим, что в нашем распоряжении имеются перчатки трех цветов: красные (К), белые (Б) и синие (С). Наугад выбираются левая и правая перчатки. Сколько различных комбинаций здесь может встретиться?

Поскольку у нас три возможности выбрать левую перчатку и столько же возможностей выбрать правую, то число различных пар составит 3×3 = 9, а именно: КК, КБ, КС, БК, ББ, БС, СК, СБ, СС.

Пусть теперь речь пойдет не о перчатках, а 6 носках такой же расцветки. В данном случае между левым и правым носком нет никакой разницы. Поэтому первым побуждением многих, очевидно, будет разделить ответ предыдущей задачи на два. Но, поскольку ⁹/₂ - не целое число, ясно, что такое решение по меньшей мере наивно. Действительно, разнородные пары можно сгруппировать по две:

КБ и БК 
КС и СК 
СБ и БС

Однако одноцветные пары можно считать лишь один раз:

КК 
ББ 
СС

Поэтому существует лишь шесть возможных комбинаций носок.

Формула, задающая число N различимых комбинаций, которая бы не принимала в расчет различия между правым и левым, запишется в виде

где Т - исходное число случаев (без учета возможных симметрии), а С - число симметричных комбинаций. Для рассмотренной нами задачи Т = 9, С = 3, так что N = ¹/₂ (9 + 3) = 6. Если обобщить эту задачу, считая, что носки могут быть а различных расцветок, получим Т = а², С = а, так что число различных пар окажется равным

Операция перемены мест левого и правого, примененная дважды, возвращает перемещаемые объекты на исходные места. Любая симметричная операция, обладающая тем же свойством, называется инволюцией. Примерами инволюций являются: вращение плоской фигуры на 180°; выворачивание чего-либо наизнанку; перемена мест верха и низа; замена любого отличного от нуля числа х обратным ему числом 1/х; замена любого числа у противоположным числом -у и т. д. Формула

задает число различимых комбинаций для произвольной инволюции. При этом, как и прежде, Т означает общее число случаев, подсчитанное без учета инволюции, а С - число случаев, которые инволюция переводит в самих себя, то есть случаев, не меняющихся при инволюции, или, выражаясь математическим языком, инвариантных относительно инволюции.

17. Разобьем трехзначные числа на группы, относя к одной группе числа, записанные одними и теми же цифрами, но в обратном порядке. (При этом некоторые числа, скажем 131, будут единственным элементом, составляющим соответствующую группу.) На сколько групп разбиваются все числа от 000 до 999?

18. Рассмотрим множество всех четырехбуквенных "слов", составленных из букв латинского алфавита, и будем считать каждое "слово" эквивалентным другому, составленному из тех же букв, но в обратном порядке. Сколько окажется неэквивалентных "слов"?

19. На цепочку нанизываются k бусинок, которые могут быть окрашены в n различных цветов. Естественно, что если перевернуть цепочку, поменяв местами ее концы, то вряд ли имеет смысл считать полученную цепочку новой. Сколько таких различных цепочек существует? (Указание: рассмотрите случаи четного и нечетного k отдельно.) Проверьте полученный ответ для случаев n = 2 и 3, a k = 4 и 5.

20. Одна сторона бумажного листа отмечается произвольной цифрой от 1 до 5, а другая - цифрой от 3 до 9. Сколько существует различных вариантов такой разметки? Никакого различия между верхом и низом листа делать не следует. (Указание: для того чтобы проверить полученный вами ответ, несложно выписать все возможные здесь варианты.)

21. Обычный набор домино содержит по одной из всех возможных костей - от 0-0 до 6-6. Рассмотрим "необычное" домино - с костями от 0-0 до 9-9. Сколько костей в этом наборе?

Предположим теперь, что в нашем распоряжении имеются карточки из картона размером примерно 3×5 см, и мы можем срезать уголки этих карточек (срезать уголок - значит удалить равносторонний прямоугольник с катетом 0,5 см и вершиной в углу карточки). Мы, разумеется, можем срезать любое число уголков - от 0 до 4 - у каждой конкретной карточки. Сколько различных вариантов "испорченных" карточек мы получим?

Без учета симметрии карточек число возможных случаев подсчитать относительно просто. Ведь в этом варианте задачи лицевую сторону карточки следует отличать от тыльной, левую сторону - от правой, верх - от низа, а потому все углы занимают четко определимые положения: их можно обозначить как правый верхний, левый верхний, правый нижний и левый нижний. Каждый из углов можно либо обрезать, либо оставить, так что, согласно теореме 1, всего возможно 2⁴ = 16 различных случаев. Однако, если считать четыре угла карточки неразличимыми, следует прибегнуть к другому рассуждению.

Стратегия "грубой силы" может заключаться в простом перечислении всех случаев:

1. Обрезанных уголков нет.

2. Обрезан один уголок.

3. Обрезаны два уголка, примыкающие к короткой стороне карточки.

4. Обрезаны два уголка, примыкающие к длинной стороне.

5. Обрезаны два противоположных уголка.

6. Обрезаны любые три уголка.

7. Обрезаны все четыре уголка.

Все семь случаев показаны на рис. 92.

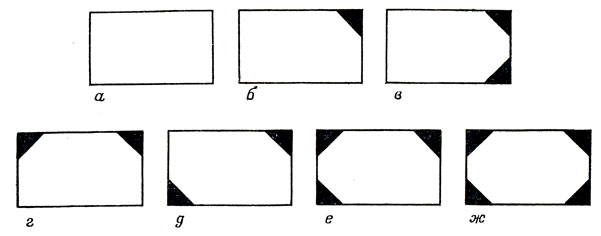
Рис. 92. Семь различных способов отрезать уголки прямоугольных карточек

Более методичная стратегия решения этой задачи основана на соображении, согласно которому симметрии рассматриваемой карточки соответствуют трем различным инволюциям:

1. Повороту карточки на 180° относительно центра (в плоскости).

2. Повороту карточки на 180° относительно горизонтальной средней линии (что приводит к переворачиванию карточки).

3. Повороту карточки на 180° относительна вертикальной средней линии (что также приводит к переворачиванию карточки).

(Строго говоря, существует еще одна симметричная операция - так называемая "единичная", или тождественная операция, при которой с фигурой ничего не происходит.)

Заметьте, что рис. 92,б и е меняются при выполнении любой из трех инволюций, в то время как рис. 92,а и ж не меняются. Кроме того, рис. 92,в не меняется при инволюции 2, рис 92,г не меняется при инволюции 3, а рис. 92,д не меняется при инволюции 1.

Чтобы подсчитать число различных комбинаций на рис. 92, мы, как и прежде, разделим исходное число случаев (2⁴ = 16) на число операций симметрии (в нашем случае четыре, включая единичную операцию). Но здесь надо быть особенно внимательным при добавлении членов, которые выражают числа карточек, симметричных по отношению к каждой из инволюций. Соответствующая формула будет иметь вид

где N - искомое число различных случаев, Т - общее число случаев, подсчитанное без учета симметрии, C₁ - число исходных карточек, не меняющихся при инволюции 1, С₂ - число исходных карточек, не меняющихся при инволюции 2, и С₃ - число карточек, не меняющихся при инволюции 3.

В рассматриваемой задаче Т = 16. Случаи, входящие в С₁, то есть не меняющиеся при повороте карточки на 180° относительно центра, должны получаться, если правый верхний угол карточки совпадает с левым нижним углом, а правый нижний угол - с левым верхним. Ясно, что таких случаев ровно четыре: пара правый верхний - левый нижний может быть либо оставлена, либо обрезана, и пара правый нижний - левый верхний может быть либо оставлена, либо обрезана. Подобным же образом и С₂ = 4, поскольку и здесь подобное рассуждение применимо к двум парам углов: правому верхнему - правому нижнему и левому верхнему - левому нижнему. Наконец, С₃ - 4, поскольку в этом случае попарно соединяются между собой отдельно верхние и отдельно нижние углы. Поэтому мы получаем

что совпадает с найденным ранее ответом.

Можно не обрезать уголки карточек, а закрашивать их разными цветами. Пусть у нас будут три цвета: красный, белый и синий (белый цвет можно рассматривать как аналог необрезанной части карточки). Тогда общее число случаев без учета симметрии равно Т = 3⁴ = 81, а С₁ = С₂ = С₃ = 3² = 9. Таким образом, для этой задачи

22. Раскрасьте 27 различных карточек, используя красные, белые и синие уголки.

23. По какой формуле вы найдете число различных карточек с цветными уголками, если для раскраски уголков можно использовать n цветов?

Вернемся еще раз к задаче о числе экипажей на автостоянке. Примем, что два колеса "эквивалентны", если они принадлежат одному экипажу. Тогда, согласно этому определению, число классов "эквивалентных" колес окажется равным числу экипажей. Колеса автомобиля расположены по вершинам прямоугольника, как и уголки в задаче о карточках. Однако симметрии прямоугольника можно привлечь не только для подсчетов, связанных с автомобилями, но, как показывает рис. 93, и для велосипедов и тачек. Поэтому С₀ (здесь - общее число колес) равно А + В + Т, то есть общему числу колес. Далее, С₁ = Т, поскольку при повороте автомобиля или велосипеда на 180° их колеса меняются местами, в то время как колесо тачки остается на месте. Аналогично С₂ = T поскольку опять-таки передние и задние колеса меняются местами (хотя и не переворачиваются как карточки). Наконец, С₃ = В + Т, поскольку при перемене левого колеса на правое колеса велосипеда и тачки остаются на месте. Поэтому мы получаем ранее выведенную формулу для числа экипажей:

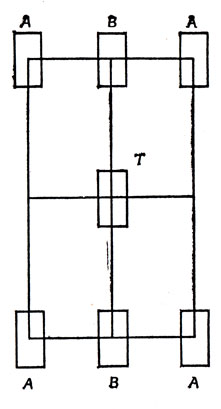
Рис. 93. Колеса автомобиля (А), велосипеда (В) и тачки(Т)

24. Из шести квадратных плиток собирается одйо гексамино размером 2×3. Плитки могут быть окрашены в пять разных цветов. Сколько типов раскраски гексамино можно получить?

25. Какие заглавные буквы английского алфавита имеют те же четыре типа симметрии, что и рассмотренные выше карточки (или любые другие прямоугольники)? Можно ли хотя бы приближенно рассматривать эти буквы как формы полимино?

26. Из черных и белых единичных квадратов складывается "лоскутный" прямоугольник размером а×b (а и b не равны). Квадраты раскрашены одинаково с обеих сторон, а прямоугольник можно перевернуть. Сколько по-разному раскрашенных прямоугольников можно получить? (Указание: рассмотрите отдельно случаи, когда а и b оба четны, оба нечетны, и случай разной четности а и b.)

Поля шахматной доски размером 2×2 окрашены в два цвета. Сколько различных случаев может нам встретиться, если мы пренебрежем вращением шахматной доски, но запретим рассматривать как совпадающие зеркально симметричные раскраски? Шесть различных способов такой раскраски указаны на рис. 94. Однако если мы разрешим рассматривать как совпадающие случаи зеркально симметричной раскраски, то число раскрасок доски не уменьшится. Если же рассмотреть ту же задачу для шахматной доски размером 3×3, то в таком варианте найдутся примеры зеркальных двойников, которые мы вынуждены будем считать различными в условиях, когда доску разрешается лишь вращать. Два подобных примера приведены на рис. 95.

Рис. 94. Различные двухцветные раскраски доски 2×2

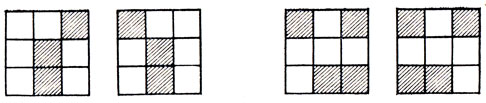
Рис. 95. Различные зеркально симметричные пары

Квадрат имеет четыре "поворотные симметрии": поворот на 0° (единичный оператор), поворот на 90°, поворот на 180° и поворот на 270° (или, что то же самое, поворот на -90°). Для того чтобы подсчитать общее число N случаев, различимых при этих преобразованиях, можно воспользоваться формулой, аналогичной рассмотренным раньше:

где С₀ - число случаев, не меняющихся при вращении на угол 9. Заметьте, что в нашем случае общее число Т случаев, подсчитанное без учета вращений, равно С₀; и всегда Т в аналогичных формулах - число случаев, которые не меняются при применении единичной или тождественной операции. Далее, мы также получаем, что С₉₀ = С₂₇₀, поскольку если какая-то наша фигура останется неизменной после поворота на 90° в одном направлении, она не изменится и при повороте на 90° в другом направлении. Поэтому нашу формулу можно переписать в виде

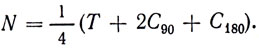
Для двухцветной шахматной доски размером 2×2 Т = = 2⁴ = 16, поскольку каждое из четырех полей может быть окрашено либо одной, либо другой краской. Далее, С₉₀ = 2, так как шахматная доска размером 2×2 не изменится при повороте на 90° только в тех случаях, когда все поля доски окажутся одноцветными. Наконец, С₁₈₀ = 2² = 4, ибо требования инвариантности при повороте на 180° влекут за собой условие одноцветности диагональных полей. Поэтому мы получаем две пары диагональных полей, каждая из которых может быть окрашена либо в один, либо в другой цвет. Подставляя найденные значения в формулу, получаем

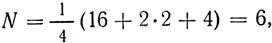
что совпадает с числом случаев, показанных на рис. 94.

27. Сколько существует различных шахматных досок размером 2×2, поля которых можно окрашивать любым из трех цветов (как и в предыдущем примере, мы считаем, что доски, получаемые одна из другой поворотом, между собой не различаются)? Проверьте свой ответ, зарисовав все возможные случаи.

28. Квадрат разбивается своими диагоналями на четыре треугольника. Для окраски этих треугольников можно использовать один из трех цветов. Считая, что вращение квадрата вокруг центра его не меняет, определите, сколько различных схем раскраски можно применить? (Совпадает ли полученный вами ответ с ответом предыдущей задачи?). Расположите найденные квадраты, образуя прямоугольник, таким образом, чтобы прилегающие треугольные области соседних квадратов были окрашены в один цвет, а треугольные области квадратов, примыкающих к границам прямоугольника, также оказались одноцветными.

29. Поля шахматной доски размером 2×2 окрашиваются в любой из четырех цветов. Доску можно поворачивать, но нельзя зеркально отображать. Сколько существует различных способов раскраски доски? Найдите общий ответ этой задачи, помня, что для раскраски полей доски разрешается применять n красок. Можете ли вы непосредственно (алгебраически) доказать, что полученной вами формулой всегда задается целое число?

30. Пусть задана двухцветная шахматная доска размером 3×3, которую можно поворачивать. Сколько существует способов раскраски такой доски? Можете ли вы изобразить все эти случаи на бумаге?

31. Сколько существует шахматных досок размером 3×3, поля которых окрашены n красками, если условиться не различать доски, полученные одна из другой поворотом?

32. Выведите общую формулу для числа различных шахматных досок размером k×k, поля которых окрашены n красками. Условимся считать, что вращение доски ее не меняет. (Указание: рассмотрите отдельно случаи четного и нечетного k.)

33. Найдите октамино, симметричное по отношению к повороту на 90°. Сколькими способами можно сложить восемь квадратных плиток, каждая из которых может быть черной или белой, с тем, чтобы образовать эту фигуру?

34. Каждая бусинка может быть одного из n цветов. Четыре бусинки нанизываются на нитку, концы которой связываются. (Полученное ожерелье, естественно, не изменится, если мы будем передвигать бусинки по нитке.) Сколько различных ожерелий можно составить?

А теперь перейдем к изучению полной группы симметрии квадрата: не только вращений, но и зеркальных отражений^*. Рассмотрим квадрат, изображенный на рис. 96. В дополнение к четырем вращениям на 0, 90, 180 и 270° относительно центра квадрата С он допускает также отражения относительно четырех осей: горизонтальной НН, вертикальной VV, первой диагональной D₁D₁ и второй диагональной D₂D₂. (Рассматриваемые восемь симметрии образуют так называемую диэдральную группу квадрата.)

^* (Ср., например, §3 статьи: Н. Я. Виленкин, И. М. Яглом, Теория групп и школьная математика, сб. "Новое в школьной математике", М., изд-во "Знание", 1972, стр. 114-146.)

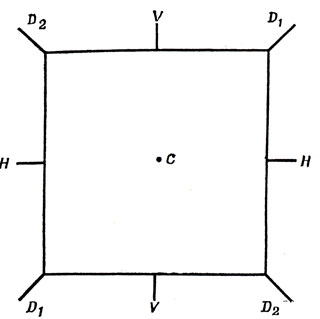
Рис. 96. Восемь симметрий квадрата

В качестве типичной рассмотрим следующую задачу. Предположим, что одно мономино (или одна фишка) ставится на поле обычной шахматной доски размером 8×8. Из рис. 97 ясно, что существует 10 неэквивалентных размещений мономино, не переходящих одно в другое при вращениях и отражениях. Этот же ответ можно получить и из формулы для числа N неэквивалентных случаев при всех (диэдральных) симметриях квадрата. Как и раньше, формула будет иметь вид

Здесь Т - общее число случаев, подсчитанное без учета симметрии, а С₉₀, С₁₈₀, С₂₇₀ имеют тот же смысл, что и в предыдущей формуле. Далее, С_V, С_H, С_D1, и С_D2 - число конфигураций, инвариантных при отражениях относительно вертикальной, горизонтальной, первой диагональной и второй диагональной осей соответственно. Как и в предыдущем примере, С₉₀ = С₂₇₀. Более того, С_V = С_H и C_D1 = C_D2, что позволяет переписать формулу в упрощенном виде.

Рис. 97. 10 неэквивалентных положений мономино на шахматной доске

Для рассматриваемой задачи Т = 64, поскольку существует в точности 64 различных варианта расположения одного мономино на шахматной доске размером 8×8. Далее, С₉₀ = 0, так как поворот на 90° обязательно переводит мономино на поле, которое ранее было пустым. По тем же соображениям С₁₈₀ = 0 и С_H = 0. Однако С_D = 8, ибо мономино может располагаться вдоль диагонали и симметричное отражение относительно диагонали оставит мономино на прежнем месте. Поэтому

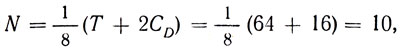
что совпадает с ответом, полученным иным способом.

В качестве другого примера рассмотрим размещение двух мономино на доске размером 4×4. В этом случае Т = (₂¹⁶) = 120. Снова С₉₀ = 0, но С₁₈₀ = 8, так как любому расположению одного мономино на нижней половине доски отвечает симметричное относительно центра доски расположение второго мономино на верхней половине доски. По аналогичным соображениям и С_H = 8. Наконец, C_D = 6 + (₂⁴) = 12, поскольку существует ровно шесть способов расположить одно мономино под диагональю, в то время как другое будет расположено симметрично ему над диагональю, и (₂⁴) способа расположить оба мономино на диагонали. Отсюда получаем общее число неэквивалентных случаев:

Эти 21 случая представлены на рис. 98.

Рис. 98. 21 различный способ поставить два мономино на доску 4×4

35. Сколькими различными способами можно расположить три мономино на шахматной доске размером 3×3? Сравните полученный вами ответ с числом предварительно сделанных чертежей, изображающих различные расположения трех мономино.

36. Сколькими способами можно расположить четыре мономино на шахматной доске размером 4×4? На доске размером 6×6? А на доске размером 8×8?

37. Сколькими способами (не переходящими один в другой при симметриях диэдральной группы) можно раскрасить тремя красками поля шахматной доски размером 4×4?

38. При игре в крестики-нолики на полях доски размером 3×3 располагаются пять крестиков и четыре нолика. Сколько всего существует вариантов расположения крестиков и ноликов?

39. Сколькими способами на шахматной доске размером 8×8 можно расположить шесть мономино так, чтобы на каждой горизонтали и каждой вертикали располагалось лишь четное число мономино? Сначала определите Т - общее число расположений, подсчитанных без учета симметрии, и лишь затем переходите к нахождению числа N решений, не эквивалентных относительно вращений и отражений квадрата.

40. Сколькими способами можно поместить одно мономино на доске размером n×n? А два мономино? (Указание: часто случаи четного и нечетного значений n полезно рассматривать отдельно.)

41. Классифицируйте 12 пентамино по типам групп симметрии, которые они допускают. Обладают ли какие-либо пентамино теми же симметриями, что и квадрат? Для каких пентамино симметриями являются лишь инволюции? Какие из пентамино допускают лишь тривиальную "единичную" симметрию?

42. Сколькими способами можно раскрасить пять квадратов, образующих Х-пентамино, используя три краски? В скольких из этих раскрасок встретятся все три цвета?

43. Сколькими способами на шахматной доске размером 4×4 можно расставить четыре ладьи так, чтобы никакие две не били одна другую? Сначала решите эту задачу без учета возможных симметрии, а затем определите число расположений, не переходящих одно в другое при вращениях и зеркальных отражениях доски.

44. Решите предыдущую задачу для случаев расположения шести ладей на доске размером 6×6 и восьми ладей на доске размером 8×8.