
Перестановки, факториалы и биномиальные коэффициенты
Пусть нам дано множество, содержащее k элементов. Из этого множества отбирается первый, второй, третий и т. д. k-й элементы. Сколькими способами это можно сделать?
Приведем примеры аналогичной постановки задач: сколькими разными способами можно разложить подряд карты колоды, состоящей из 52 карт; сколькими способами можно переставить буквы А, Б, В, Г, Д и т. д.
Ответы на все подобные вопросы дает следующая
Теорема 2. Число способов, которыми данные k элементов можно расположить в определенном порядке {то есть выбрать первый из них, затем второй, третий и т. д. до k-го), равно произведению
1×2×3× ... ×(k-1)×k.
(Это произведение обозначается k! и, как мы уже говорили, читается как "k-факториал".)
Доказательство. Выбор первого элемента можно произвести k способами. После этого для второго элемента остается (k-1) возможность, для третьего - (k-2) и т. д. Поэтому упорядочение всех k элементов может быть произведено
k·(k-1)(k-2)· ... ·2-1 = k!
различными способами.

Поскольку 3! = 6, то существует ровно шесть способов расположения в ряд трех букв, например О, Р и Т, а именно: ОРТ, ОТР, РОТ, РТО, ТОР, ТРО. Аналогично если вам даны любые пять букв, то существует ровно 5! = 120 различных составленных из этих букв "слов". Небезынтересна такая игра: для k = 2, 3, 4, 5 или 6 подыскать такие наборы из k букв, чтобы среди всевозможных перестановок этих букв отыскалось как можно больше осмысленных слов. Для слов английского языка (и букв латинского алфавита) уже при k = 4 затруднительно отыскать набор из четырех букв, дающий более пяти осмысленных слов из возможных 24; для слов же из пяти букв как будто бы лучшим результатом является 8 из 120.
Справедливо соотношение (k+1)·k! = (k+1)!, поскольку произведение всех натуральных чисел от 1 до k, умноженное на (k+1), дает произведение всех чисел от 1 до (k+1). Отсюда получается соотношение
| k! = | (k+1)! | . |
| k+1 |
Если положить в этом соотношении формально k = 0, то мы получим
| 0! = | 1! | = 1. |
| 1 |
Поэтому 0! по определению полагается равным 1. (Заметим, что исходное определение не включало случай k = 0, и поэтому для k = 0 требуется отдельное определение.)
Для приближенного вычисления факториалов применяется знаменитая формула Стирлинга:
k! ~ √2πk (k/e)k.
В эту формулу входят обе вездесущие математические константы: π = 3,14159 ... - отношение длины окружности к диаметру и е = 2,71828... - основание "натуральных логарифмов". Знак радикала √, как обычно, показывает на необходимость извлечения квадратного корня. Знак ~ можно прочесть как "приближенно равно". Здесь это означает, что при стремлении k к бесконечности обе части формулы Стерлинга становятся все ближе и ближе друг к другу, иными словами, что их отношение будет стремиться к 1. Для каждого конкретного значения k формула Стерлинга дает приближенное значение k!, причем с возрастанием k относительная погрешность такого приближения становится все меньшей. Вывод формулы Стерлинга выходит за рамки комбинаторного анализа, и по этой причине мы не будем воспроизводить его в нашей книге*. Мы только покажем, как "работает" эта формула при решении комбинаторных задач.
* (Элементарное (но вовсе не простое) доказательство формулы Стирлинга имеется в книге: А. М. Яглом и И. М. Яглом, Неэлементарные задачи в элементарном изложении, М., Гостехиздат, 1954 (см. задачи 160-161 на стр. 80 и их решение).)
Рассмотрим, например, задачу о числе способов расположения в ряд всех карт полной колоды из 52 карт. Мы уже знаем, что искомое число равно 52!, и по формуле Стерлинга можем приближенно его оценить:
52! ≈ √104π(52/e)52 ≈ 18,076×(19,130)52 ≈ 8,054×1067.
Такое приближение достаточно для большинства задач, ибо, когда мы имеем дело со столь большими числами, нет необходимости знать точно все их цифры.
Предположим теперь, что нам задано множество, состоящее из k элементов, и мы последовательно отбираем из него r элементов, обозначая их как первый, второй, третий и т. д. до r-го. Число способов отобрать различные r-элементные последовательности из множества в k элементов обозначают через Akr или через (k)r*.
* (А - первая буква французского слова arrangement, что означает упорядочение или размещение.)
Теорема 3.
Akr = k!/(k-r)! = k(k-1)(k-2) ... (k-r+1).
Доказательство. Первый элемент последовательности можно отобрать k способами, второй элемент (k-1) способами, произвольный элемент с номером i можно отобрать k-(i-1) = k-i+1 способами. В частности, последний r-й элемент последовательности можно отобрать k-r+1 способами. Поэтому общее число всех возможных таких последовательностей равно
k(k - 1)(k - r) ... (k - r + 1).
А поскольку это число равно произведению всех натуральных чисел от 1 до k за вычетом чисел от 1 до (k - r) то его можно представить в виде k!/(k - r)!.
Упражнения
3. В некотором испытании следует угадать три различные буквы алфавита и выписать их на доске в определенном порядке. Правилам удовлетворяет лишь одна комбинация букв. Сколько существует "неправильных" комбинаций?
4. Каждому из шести игроков сдается по одной карте из колоды, содержащей 52 различные карты. Сколько может быть вариантов сдачи?
Теперь рассмотрим такую ситуацию: при игре в покер одному игроку сдаются одновременно пять карт из полной колоды в 52 карты. Таким образом, в руках игрока оказываются пять карт, причем ему, разумеется, безразличен порядок их появления. Поэтому число "покерных" сдач одному игроку равно числу способов отобрать неупорядоченную комбинацию пяти карт из общего числа 52 карт. Аналогично число возможных сдач игроку при игре в бридж равно числу способов выбора неупорядоченного набора из 13 карт из общего множества в 52 карты. В общем случае, если задано множество из k объектов, из которого отбираются r, то число неупорядоченных наборов r объектов из исходного множества в k объектов обозначается через Сkr или (kr)*.
* (С - первая буква французского слова combinaison, что означает комбинацию или сочетание.)
Теорема 4.
Ckr = k(k - l)(k - 2) ... (k - r + 1) / r(r - 1)(r - 2) ... 2·1 = (k)r / r! = k! / r!(k - r)!.
Доказательство. Число упорядоченных наборов г элементов из множества, содержащего k элементов, равно Аkr. Выбранные r объектов могут быть переставлены r! способами, и все эти перестановки отвечают одному неупорядоченному набору r элементов. Поэтому число неупорядоченных наборов равно Аkr/r!. Используя теорему 3, мы получаем, что искомое число равно
k! / r!(k - r) или k(k - 1)(k - 2) ... (k - r + 1) / r(r - 1)(r - 2) ... 2·1.
По теореме 4 число возможных сдач карт одному игроку в покер равно
С525 = (525 ) = 52·51·50·49·48 / 5·4·3·2·1 = 2598960,
а число сдач одному игроку в бридж равно
С5213 = (5213 ) = 52·51·50·49·48·47·46·45·44·43·42·41·40 / 13·12·11·10·9·8·7·6·5·4·3·2·1 = 635013559600.
Упражнения
5. Сколькими способами можно расположить четыре мономино на шахматной доске размером 8×8?
6. Сколькими способами на обычной шахматной доске можно расставить восемь ферзей?
7. Сколькими способами можно выбрать шесть пентамино из набора, содержащего 12 различных пентамино?
8. Клуб устраивает свои вечерние собрания три раза в неделю. Сколькими способами члены клуба могут выбрать дни недели для встреч?
Согласно известной в алгебре формуле бинома Ньютона,
(x + y)k = xk + (1k) xk-1y + (2k) xk-2y2 + (3k) xk-3y3 + ... + (k-1k) xyk-1 + yk.
По этой причине числа Сkr или (rk) называют биномиальными коэффициентами (коэффициентом в алгебре обычно называют числовой или буквенный множитель перед произведением переменных). Используя приведенное выше определение чисел Сkr, читатель может попробовать самостоятельно доказать формулу бинома Ньютона.
Поскольку вряд ли имеет смысл обсуждать вопрос о числе тех подмножеств исходного множества из k элементов, которые вовсе не содержат никаких элементов, то уславливаются, что существует лишь одно такое пустое подмножество. Это соглашение не противоречит теореме 4, ибо при формальной подстановке в ее результат значения r = 0 мы получаем
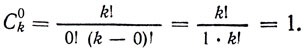
Поэтому начальный член биномиальной формулы xk можно рассматривать как имеющий коэффициент Сk0, а последний член yk - как имеющий коэффициент (kk) (или Сkk).
Французский математик XVIII века Блез Паскаль расположил биномиальные коэффициенты в таблицу, имеющую вид треугольника:
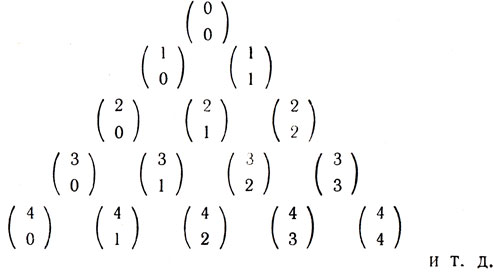
Этот треугольник известен под названием "треугольник Паскаля"*. Если вместо биномиальных коэффициентов подставить их числовые значения, то становится понятным его "устройство": каждый элемент "треугольника" равен сумме двух стоящих над ним.
* (См. рассчитанную на школьников брошюру: В. А. Успенский, Треугольник Паскаля, М.,.изд-во "Наука", 1966. Оригинальный мемуар Паскаля с обстоятельными комментариями изложен в книге: Дж. Пойа, Математическое открытие, М., изд-во "Наука", 1970, гл. 3.)

Со времен Паскаля были открыты сотни свойств элементов этого числового треугольника. Некоторые из них мы предлагаем читателю для доказательства в качестве упражнений.
Упражнения
1. Суммы элементов строк треугольника Паскаля есть последовательные степени двойки, то есть
(0k) + (1k) + (2k) + ... + (kk) = 2k.
2. Знакочередующиеся суммы элементов любой строки равны нулю (в знакочередующейся сумме первый элемент берется со знаком плюс, второй - со знаком минус, третий - со знаком плюс, четвертый - со знаком минус и т. д.). Таким образом,
(0k) - (1k) + (2k) - (3k) ± ... ± (kk) = 0.
3. Любой элемент равен сумме двух других, расположенных над ним (так сказать, сумме своих северо-западного и северо-восточного соседей). Это обстоятельство можно записать в виде следующей формулы:
(rk) = (r-1k-1) + (rk-1).
4. Любая строка симметрична относительно своей середины, то есть
(rk) = (k-rk).
5. Сумма квадратов элементов любой строки равна центральному элементу вдвое более далекой от вершины строки (если не считать верхнего ряда, состоящего из одной единицы). Другими словами,
(0k)2 + (1k)2 + (2k)2 + (3k)2 + ... + (kk)2 = (k2k).
Теперь мы можем получить ответ на поставленный ранее вопрос: каково число неупорядоченных комбинаций ("слов"), содержащих по n символов, составленных из знаков исходного алфавита, в который входят k символов?
Теорема 5. Число возможных неупорядоченных комбинаций n символов, составленных из знаков k-символьного алфавита, равно
(nk+n-1) = (k-1k+n-1).
Доказательство. Для того чтобы пояснить метод доказательства этой теоремы, рассмотрим сначала один типичный пример. Пусть задан алфавит, содержащий четыре буквы: а, b, с и d. Образуем из этих букв одну комбинацию, состоящую из 7 элементов, например cadbaab. Запишем эту комбинацию в "стандартной" форме:
ааа|bb|с|d.
Поскольку мы рассматриваем лишь неупорядоченные комбинации, то такая "стандартная" запись не отличается от исходной. В общем случае стандартная запись комбинации символов образуется следующим образом: для произвольной комбинации из n символов мы сначала выписываем первый символ (первую "букву" алфавита) "столько раз, сколько раз он встречается в нашей комбинации. Затем ставим вертикальную черту, после чего выписываем все вхождения второго символа, второй "буквы" алфавита и т. д. Если в исходной комбинации какой-нибудь символ алфавита отсутствует, то между соответствующими разделительными вертикальными линиями не указывается ничего.
Назовем символы алфавита и вертикальные линии отметками. В общем случае таких отметок будет n+k-1. Для нашего примера n+k-1 = 7+4-1 = 10 отметкам. Для того чтобы полностью описать стандартную форму той или иной комбинации, достаточно указать, на каких (n-1) местах из общего числа (n+k-1) мест стоят разделительные линии. Так, если в последовательности 10 отметок ---------- четвертая седьмая и девятая отметки суть разделительные линии, то последовательность имеет вид ---|--||-|-, что автоматически приводит к комбинации aaa|bb||c|d. Если же известно, что разделительными линиями являются первая, четвертая и пятая отметки, то мы получаем |--|-----|, чему соответствует комбинация |bb||ddddd.
Таким образом, различные выборы мест для разделительных линий приводят к различным неупорядоченным комбинациям, заданным в стандартной форме. Согласно теореме 4, существует ровно (k-1n+k-1) способов выбрать (k-1) из (n+k-1) отметок для разделительных линий. Следовательно, это же число равняется числу неупорядоченных комбинаций n символов, составленных из знаков k-символьного алфавита. Наконец,
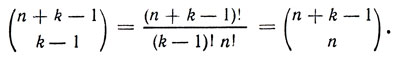
Примеры
1. Число неупорядоченных комбинаций, состоящих из пяти двоичных цифр, равно (55+2-1) = (56) = 6. В стандартной форме они суть 00000|, 0000|1, 000|11, 00|111, 0|1111 и |11111. Каждой из этих неупорядоченных комбинаций соответствуют одна или несколько упорядоченных, как показано ниже. При этом две разные упорядоченные комбинации соответствуют одной и той же неупорядоченной комбинации тогда, когда они состоят из одного и того же числа единиц (и соответственно нулей).

Заметьте, что число упорядоченных комбинаций в последовательных группах, соответствующих неупорядоченным комбинациям, образует строку треугольника Паскаля: 1 5 10 5 1.
3. Число неупорядоченных комбинаций трех букв, которые взяты из трехсимвольного алфавита, состоящего из букв а, б и в, равно
(33+3-1) = (35) = 10.
Эти комбинации суть ааа, ааб, аав, абб, абв, авв, ббб, ббв, бвв, ввв.
Упражнения
9. Определите число всевозможных четырехбуквенных неупорядоченных комбинаций элементов пятибуквенного алфавита и выпишите все эти комбинации.
10. В продаже имеются наборы фруктов, в которые входят яблоки, апельсины и груши. В каждый набор входят 12 фруктов; любой набор стоит один доллар. Сколькими разными способами может выбрать покупатель набор фруктов, причитающийся ему за его доллар?
11. Пусть задано k символов, принадлежащих разным гипам. При этом имеется k1 символов первого типа, k2 символов второго типа, k3 символов третьего типа, ..., kr символов последнего, r-го типа. (Разумеется, k1 + k2 + k3 + ... + kr = k.) Покажите, что число различных перестановок этих k символов равно
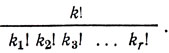
12. Используйте результат предыдущей задачи для того, чтобы определить число всевозможных перестановок букв, составляющих слова окорок и Миссисипи.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'