Комбинации

Существует 10 способов выбрать одно число среди чисел от 0 до 9. Существует 10² = 100 способов выбрать пару таких чисел. Каждую такую пару можно рассматривать как одно двузначное число из последовательности 00, 01, 02, 03, ... , 97, 98, 99. Аналогично существует 10³ = 1000 способов отобрать тройку чисел от 0 до 9, и каждую такую тройку можно рассматривать как элемент последовательности трехзначных чисел от 000 до 999. В общем случае существует 10ⁿ способов отобрать упорядоченный набор n чисел от 0 до 9. А так как дело заключается не в обозначениях и ничто не зависит от того, обозначаем мы отбираемые элементы цифрами 0, 1, 2, ... ,9 или буквами А, Б, В, ..., З, И, символами а₁, а₂, а₃, ..., а₁₀ или каким-то другим образом, то наш вывод можно обобщить: существует ровно 10ⁿ способов отобрать упорядоченный набор n символов из любого данного набора из 10 различных символов.

Если же исходное множество символов, из которого мы выбираем элементы, содержит k различных символов, а мы формируем из этих элементов упорядоченные последовательности (или цепочки) длины n, то число различных упорядоченных наборов n символов будет равно kⁿ.

Например, если исходное множество состоит всего из двух элементов - 0 и 1 - и мы образуем всевозможные последовательности, содержащие по четыре таких элемента, то k = 2, n = 4 и число таких последовательностей равно kⁿ = 2⁴ = 16. Эти последовательности будут не чем иным, как представлением в двоичной системе счисления целых чисел от 0 до 15:

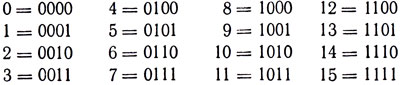
(В этой таблице слева от знака равенства стоят десятичные числа, а справа - их двоичные эквиваленты.) Двоичная система счисления имеет всего две цифры - 0 и 1; она применяется в электронных вычислительных машинах^*.

^* (По этому поводу см., например, брошюру: С. В. Фомин, Системы счисления, М., изд-во "Наука", 1968, в частности, §§ 8 и 12-13.)

Еще более общее утверждение о комбинациях дает следующая

Теорема 1. Пусть дано n множеств, причем первое из них содержит k₁ элементов, второе - k₂ элементов и т. д., наконец, n-е содержит k_n элементов. Число различных n-элементных последовательностей, первый элемент которых принадлежит первому множеству, второй - второму и т. д., n-й элемент - n-му множеству, равно k₁×k₂× ... ×k_n.

В частности, если все n множеств совпадают, то k₁ = k₂ = ... = k_n = k и число всевозможных комбинаций равно

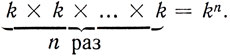
Доказательство. На первое место в последовательности может быть поставлен любой элемент первого множества. Поэтому выбор первого элемента последовательности можно осуществить k₁ способами. Для каждого из них выбрать второй элемент из второго множества можно k₂ способами. Поэтому пару элементов из первых двух множеств можно выбрать k₁k₂ способами. Для каждого из этих k₁k₂ способов существует k₃ способа выбрать третий элемент из третьего множества, так что число возможных троек равно k₁k₂k₃. Продолжая рассуждать подобным же образом, мы получим, что существует всего k₁k₂ ... k_n способов выбрать по одному элементу из каждого из наших n множеств.

В качестве иллюстрации применения теоремы 1 рассмотрим такую задачу. Номер автомобиля в некотором государстве состоит из двух букв и четырех цифр. Буквы берутся из латинского алфавита (содержащего 26 букв), а цифры могут принимать любое значение от 0 до 9. Сколько может быть выдано различных автомобильных номеров?

Непосредственное применение теоремы 1 дает ответ:

26×26×10×10×10×10 = 6760000 номеров.

Большую трудность представляет вопрос о числе неупорядоченных комбинаций n символов, взятых из исходного "алфавита", содержащего k символов. Говоря о неупорядоченных комбинациях, мы имеем в виду, что нам безразличен порядок, в котором символы входят в ту или иную комбинацию. Например, если мы отбираем четыре символа из двоичной системы, в которой есть лишь 0 и 1, и не обращаем внимания на порядок, то получаем всего пять различных случаев: 0000, 0001, 0011, 0111, 1111. Разительное расхождение со случаем упорядоченных комбинаций, где мы только что выписали 16 различных упорядоченных четверок!

Если не обращать внимание на порядок, то при бросании, скажем, двух одинаковых игральных костей может осуществиться не 36, а всего 21 исход, поскольку, например, исходы (1, 4) и (4, 1) для нас неразличимы. (Естественно, что при бросании двух костей могут получиться всего 11 значений суммы выпавших очков, так как существует всего 11 целых чисел в интервале между 2 и 12. При этом сумма 7, например, может получиться в трех случаях - как 3+4, как 2+5 и как 1+6.) Но отложим пока решение вопроса о числе неупорядоченных комбинаций, а до этого введем кое-какие необходимые вспомогательные понятия.

1. Телефонный номер состоит из семи цифр, причем первые две могут быть любой цифрой от 2 до 9, а остальные - произвольны, то есть могут принимать все значения 1, 2, ..., 9, 0. Сколько существует возможных различных телефонных номеров?

(Ответы на все упражнения этой главы можно найти в Приложении 1.)

2. В школе шесть классов, в которых обучаются соответственно 12, 15, 9, 13, 11 и 12 учащихся. В ученический комитет входит по одному школьнику от каждого класса. Сколькими способами можно выбрать ученический комитет этой школы?