Конфигурация Герберта Тэйлора

Математик Герберт Тэйлор, работающий в компании "Норт Америкэн авиэйшн" (Калифорния), предложил конфигурацию, изображенную на рис. 71. Доказательство невозможности ее заполнения пентамино получено независимо Джоном Г. Флетчером из Калифорнийского университета в Беркли и Спенсером Эрншоу из колледжа в Санта-Моника (Калифорния). Приводимое нами доказательство представляет собой некоторое упрощение доказательств этих авторов.

Рис. 71. Конфигурация Герберта Тэйлора

Предположим, что существует покрытие конфигурации, изображенной на рис. 71, 12 различными пентамино. Заметим, что при размещении пентамино на этой своеобразной "доске" никакое пентамино не может отрезать от доски часть, содержащую не кратное пяти число "полей": если бы это произошло, то покрытие сразу же стало бы невозможным. Рассмотрим сначала, где может в гипотетическом покрытии располагаться X-пентамино. Легко заметить, что существуют всего два принципиально разных положения X-пентамино, если не брать в расчет случаи, им симметричные. Эти положения изображены на рис. 72.

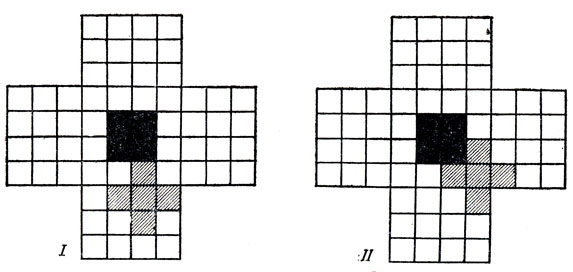
Рис. 72. Два возможных положения Х-пентамино

Для случая I исследуем возможные положения I-пентамино. Нетрудно проверить, что, как бы мы ни располагали I-пентамино, оно всегда отсечет часть доски, содержащую не кратное пяти число полей. Следовательно, случай I тупиковый.

Для случая II существуют два несимметричных положения I-пентамино, показанные на рис. 73: здесь "площади" отсекаемых частей кратны пяти, в то время как все другие расположения не удовлетворяют этому условию.

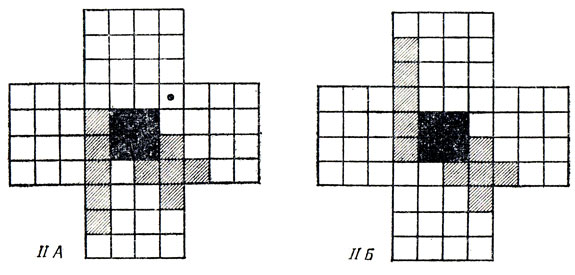
Рис. 73. Два возможных положения I-пентамино в случае II

В случае IIА рассмотрим, какие пентамино, закрывающие отмеченное точкой поле, могут заходить в "восточное" крыло фигуры. Здесь существуют три различных варианта (рис. 74).

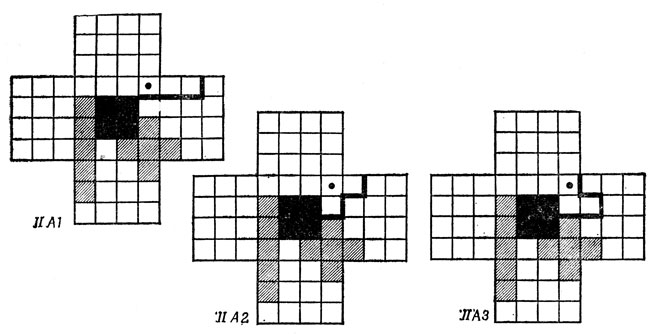
Рис. 74. Отмеченный точкой квадрат в случае IIА можно покрыть тремя способами

В случае IIA1 незаполненные части "южного" и "восточного" крыльев одинаковы, и любая из них может быть покрыта либо парой Р- и L-пентамино, либо парой W- и Y-пентамино, но не иначе. Поэтому мы вынуждены использовать Р-, L-, W- и Y-пентамино (например, так, как указано на рис. 75). Поле, отмеченное точкой, может быть покрыто либо N-, либо V-пентамино. Однако если мы будем искать место для Т-пентамино, то придем к единственно возможному расположению, указанному на рис. 75. В этом случае необходимо, чтобы поле, отмеченное точкой, было покрыто V-пентамино. Но теперь рядом с Т- следует поместить Р-пентамино, - а оно уже было использовано ранее. Тем самым случай IIА1 можно считать исчерпанным. (Нумерация пентамино на рис. 75 относится к порядку, в соответствии с которым они располагались на "доске".)

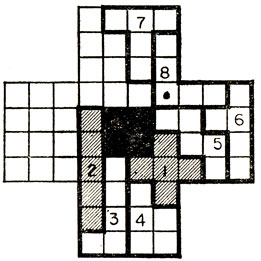
Рис. 75. Развитие случая IIA1

В случае IIA2 "южное" крыло, как и раньше, можно заполнить либо парой Р и L, либо парой W И Y. "Восточное" же крыло можно заполнить парами W и Р или L и Р. Единственная возможность заполнения одновременно обеих областей заключается в том, что W и Y покрывают "южную" часть, a L и Р - "восточную" (рис. 76). Поле, отмеченное точкой, может быть покрыто лишь F-пентамино в любой из двух его ориентации. Далее, N-пентамино необходимо расположить так, как показано на рис. 76, - после чего не остается возможности разместить Т-пентамино, что и исчерпывает случай IIA2.

Рис. 76. Развитие случая IIА2

В случае IIА3 "южное" крыло опять-таки можно заполнить либо парой Р и L, либо парой W и Y, в то время как "восточное" крыло заполняется либо парой V, F, либо парой U, L. Далее, существуют четыре возможности для расположения Т-пентамино (исключая очевидные тупиковые положения), показанные на рис. 77. В случае IIА3а поля, отмеченные точкой и звездочками, нельзя покрыть ни одним из пентамино, поскольку W уже использовано, а N отсекает два поля. В случае IIА3б для покрытия точки должно быть использовано N-пентамино, после чего уже нельзя правильно расположить Z. В случае IIА3в точку должно покрыть L, и тогда поле слева от точки покрыть уже нечем. В случае IIА3г независимо от того, какая из пар - V и F или U и L - выбирается для заполнения "восточного" крыла, точку может покрыть только Z, после чего очевидным образом покрытие завершить не удастся. Поэтому случай IIА3 также невозможен что и завершает исследование случая IIА.

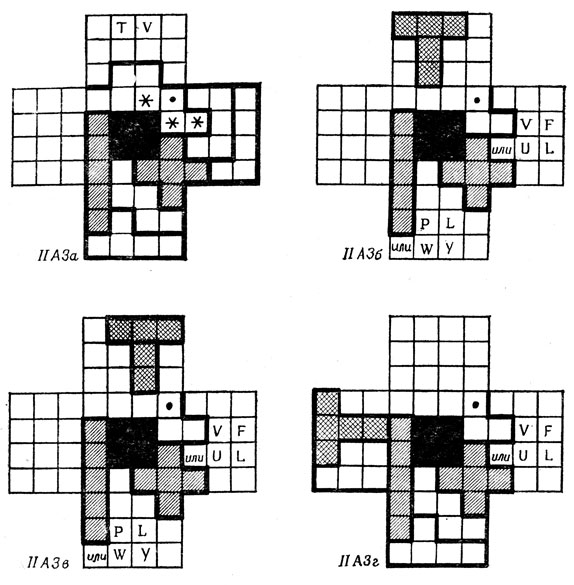
Рис. 77. Четыре возможных положения Т в случае IIA3

Остается случай IIБ. В нем существуют ровно четыре возможных положения N-пентамино, показанные на рис. 78. Для варианта IIБ1 Т-пентамино может быть расположено, лишь как на рис. 79. После этого "северное" крыло можно покрыть только с помощью Р-пентамино. Поскольку оно таким образом оказывается занятым, "южное" крыло должно быть покрыто парой W и Y, а "западное" - V и Z. Теперь отмеченное звездочкой поле на рис. 79 уже нельзя покрыть ни одним из оставшихся пентамино, что полностью исчерпывает случай IIБ1.

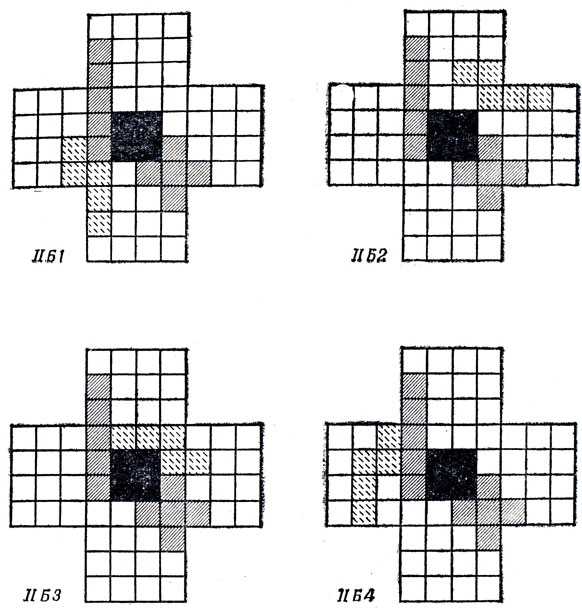
Рис. 78. Четыре положения N-пентамино в случае IIБ

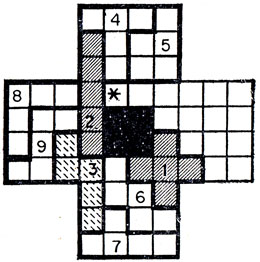
Рис. 79. Единственно возможное расположение Т в случае IIБ1

В случае IIБ2 "северное" крыло можно покрыть парой U и L, а "восточное" - W и Y (поскольку L уже использовано). Единственно возможное положение для Т-пентамино - в "восточном" крыле (рис. 80), после чего Z-пентамино (поместить уже негде, и, следовательно, случай IIБ2 также оказывается тупиковым. В случае IIБ3 "западное" крыло можно закрыть либо U, L, либо F, V, а "северное" - либо U, Y, либо Р, Т (рис. 81). (Если использовать Р для размещения в "северном" крыле вместе с V, Y, Z или L, то мы не сможем разместить Т.).

Рис. 80. Единственное допустимое положение Т в случае IIБ2

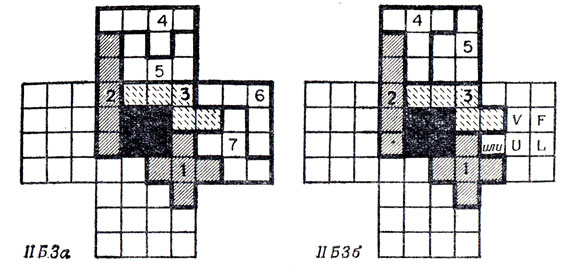
Рис. 81. В случае IIБ3 'северное' крыло необходимо заполнить либо парой U и Y, либо парой Р и Т

В случае IIБ3а существует лишь один способ расположения Т-пентамино в "западном" крыле (рис. 82), - после чего Z некуда будет поставить. Рассматривая случай IIБ3б, мы обнаруживаем два способа расположения Z-пентамино, показанные на рис. 83. В случае IIБ3бi в оставшихся свободными частях не удается расположить W-пентамино. Случай же расположения Z, как в IIБ3бii, требует, чтобы V было помещено в "западном" крыле, так что "восточное" крыло заполняется парой U и L. Остается единственный способ расположения Y-пентамино, а уж после этого F некуда ставить. Этим подводится итог случаю IIБ3б, а следовательно, и случаю IIБ3 в целом.

Рис. 82. Некуда поставить Z-пентамино

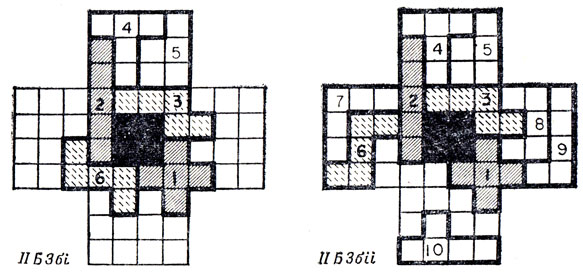
Рис. 83. Две возможности для размещения Z в случае IIБ3б

Наконец, случай ПБ4 исчерпывается наблюдением, что Т должно располагаться в "северном" крыле над I, что вынуждает поставить Р за Т, а ниже - Y. Огедовательно, "восточное" крыло заполнить уже невозможно. Так заканчивается перебор всех вариантов случая IIБ, а с ним и случая II: ответ на вопрос о возможности покрытия конфигурации, изображенной на рис. 71, оказывается отрицательным. На рис. 84 показана графическая схема всех только что разобранных случаев и подслучаев.

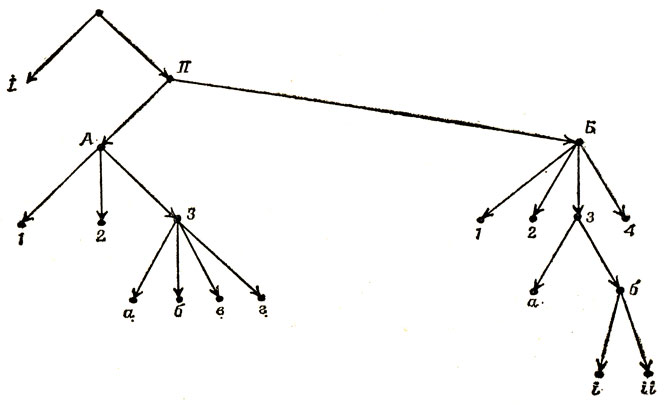
Рис. 84. Схема доказательства невозможности покрытия конфигурации Герберта Тэйлора