Зубчатый квадрат

Р. М. Робинсон предложил "решение" проблемы покрытия "зубчатого квадрата", изображенного на рис. 85. Аналогичное "решение" было также найдено Спенсером Эрншоу. Оба решения длиннее и сложнее, чем изложенное выше для предыдущей задачи. Осуществить перебор здесь можно в восемь этапов, которые мы вкратце и опишем.

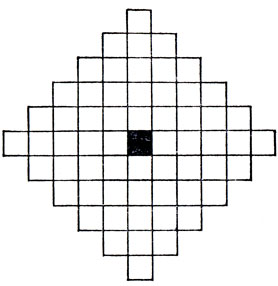
Рис. 85. Зубчатый квадрат Р. М. Робинсона

1. Углы зубчатого квадрата (см. рис. 85) могут закрыть лишь восемь из 12 пентамино (W, X, Y, F, I, L, Р, N).

2. Существует ровно 70 (ибо 8! / 4!4! = 70) способов отобрать из этих восьми полимино четыре для расположения в углах. (Формула для числа способов отобрать четыре объекта из данных восьми - это теорема 4 из следующей главы. Там же в примечании к условию теоремы 2 разъяснен смысл символа n!, читаемого как n-факториал.) В приводимой ниже таблице дано максимальное число закрываемых любым пентамино полей по краям доски (но не в ее углах) отдельно для случаев, когда пентамино закрывает и когда оно не закрывает угловую клетку. По ней для любого набора пентамино, расположенных по углам, можно найти максимальное соответствующее ему число покрываемых краевых полей.

3. На рис. 86 отмечены поля, относящиеся к четырем различным типам. Топологически все закрашенные поля - угловые, краевые и примыкающие к внутреннему полю - образуют границу конфигурации зубчатого квадрата. Основная идея "решения" Эрншоу сводится к тому, чтобы исследовать варианты покрытия этих 24 полей.

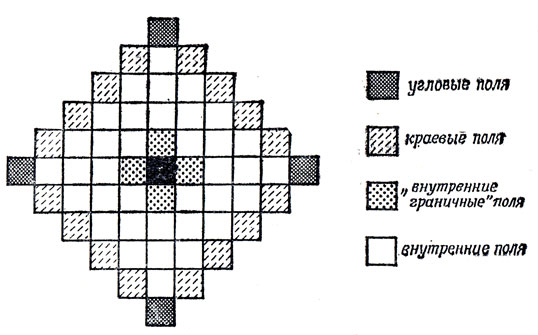
Рис. 86. Четыре типа полей зубчатого квадрата

Особо следует отметить, что лишь четыре пентамино (V, Z, I и L) могут одновременно закрывать "внутреннее граничное" поле и максимальное число угловых или краевых полей.

4. V- и I-пентамино нельзя расположить, покрывая угловые или краевые и одновременно "внутренние граничные" поля, не нарушив принципа "кратности пяти", согласно которому площади изолируемых частей должны быть кратны пяти, иначе их нельзя будет покрыть пентамино. Это обстоятельство иллюстрируется рис. 87: здесь показаны варианты совместного расположения V- и I-пентамино, причем I располагается двумя способами, а V занимает различные неэквивалентные положения относительно I, связывая "внутренние граничные" и краевые поля. Во всех вариантах принцип "кратности пяти" нарушается.

Рис. 87. 16 вариантов совместного расположения V- и I-пентамино, в каждом из которых нарушается принцип 'кратности пяти'

5. Остается всего 15 способов выбора пары из V, Z, I и L для одновременного покрытия краевых или угловых и "внутренних граничных" полей. (Строго говоря, отобрать пару из четырех элементов можно шестью способами, но этим наборам могут отвечать различные положения на "доске".) Предварительный подсчет по числу покрываемых граничных полей показывает, что остается надеяться лишь на пару I- и Z-пентамино.

6. Изучается случай, когда I и Z вместе покрывают как угловые или краевые, так и "внутренние граничные" поля. Отсюда можно сделать некоторые выводы, относящиеся к числу покрываемых полей (например, F и X должны покрыть два из четырех угловых полей). Наконец, показывается, что пара I и Z покрывает ровно одно "внутреннее граничное" поле и одно поле на наружной границе, в то время как другие пентамино (Т, V или L) должны покрыть два остающихся "внутренних граничных" поля.

7. Допущение о том, что эти поля покрываются V-пентамино, приводит к противоречию во всех вариантах (рис. 88).

Рис. 88. V-пентамино нельзя закрыть два оставшихся 'внутренних граничных' поля

8. Другие, предположения о покрытии этих полей также приводят к противоречиям. Этим завершается доказательство невозможности покрытия пентамино изображенного на рис. 85 "зубчатого квадрата".

Мы предлагаем читателю воспользоваться приведенной схемой и попытаться воспроизвести доказательство во всех деталях. Если же он сумеет найти краткую процедуру, приводящую к тем же выводам, то это будет значительным достижением.

Если мы разрешим передвигать черное мономино внутри зубчатого квадрата, то можно будет поставить задачу о покрытии остающихся 60 полей 12 пентамино; но и такое покрытие никем не было обнаружено. На рис. 89 показана конфигурация пентамино, наиболее близкая к зубчатому квадрату. Правда, любитель математических развлечений англичанин Дж. А. Линдон, обнаружил "почти требуемое" покрытие, но в его решении, приведенном на рис. 90 черное мономино располагается на краю доски.

Рис. 89. Наиболее близкая к зубчатому квадрату конфигурация пентамино

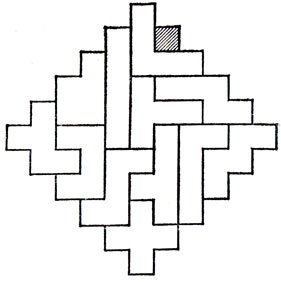
Рис. 90. Зубчатый квадрат можно покрыть пентамино, если сдвинуть отверстие к краю