Глава IV. Невозможные конструкции и метод перебора

Метод перебора

Для того чтобы доказать невозможность того или иного расположения полимино, приходится прибегать к методу, называемому систематическим перебором. Суть его заключается в том, что мы последовательно развиваем какую-то линию в решении задачи, пока либо не добьемся успеха, либо попадем в тупик. В последнем случае мы переходим к другой линии и так продолжаем до тех пор, пока не решим задачу или переберем все варианты и докажем, что решение невозможно. В этой главе методом перебора будут решены две очень трудные задачи о расположении полимино. Однако прежде подробнее обсудим сам метод доказательства.

Идею перебора иллюстрирует решение типичной задачи о лабиринте. Если человек, находящийся в точке X лабиринта, изображенного на рис. 68, изберет стратегию "идти, касаясь стены правой рукой", то он выйдет из лабиринта по пути, указанному точками. Результативность подобной стратегии зависит от устройства лабиринта. Так как в лабиринте нет изолированных стен и "островков", то, следуя указанной стратегии, нельзя дважды попасть на одно и то же место, - а это одна из характерных сторон метода перебора. Кроме того, мы, естественно, предполагаем, что человек в состоянии определить момент выхода из лабиринта, то есть распознать решение задачи. Если это не так, то, выйдя из входа с правой стороны и по-прежнему придерживаясь стенки правой рукой, он обойдет весь лабиринт и снова войдет в него через вход, но уже с другой стороны.

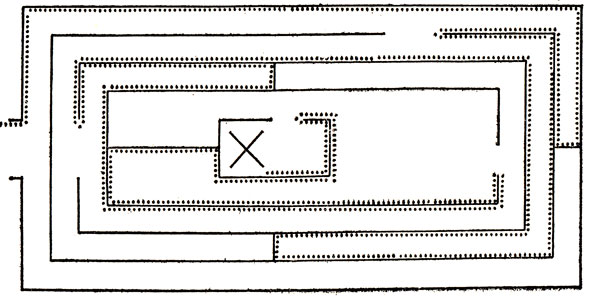
Рис. 68. Выход из лабиринта

Другим примером перебора является решение классической комбинаторной задачи о размещении на шахматной доске восьми ферзей так, чтобы никакие два не били друг друга, другими словами, не оказались на одной горизонтали, вертикали или диагонали доски. Вряд ли целесообразно исследовать все способы расположения восьми ферзей на доске и искать среди них удовлетворяющие нашему условию: число всех возможных расположений, вычисленное методами, о которых мы будем говорить в гл. V, равно 4426165368. Видимо, лучше отвести каждому ферзю свою горизонталь и пытаться последовательно располагать ферзей на неатакованных полях своих горизонталей.

Поставим первого ферзя на произвольное поле первой горизонтали. Для того чтобы скорее прийти к требуемому расположению, лучше сначала избрать для него какое-нибудь "типичное" (среднее) поле, скажем отмеченное единицей на рис. 69, а. Второго ферзя поставим на произвольное неатакованное поле второй горизонтали; для систематичности выберем самое правое из всех возможных полей. Аналогичным образом поступим с третьим, четвертым, пятым и шестым ферзем и придем к расположению, показанному на рис. 69, а.

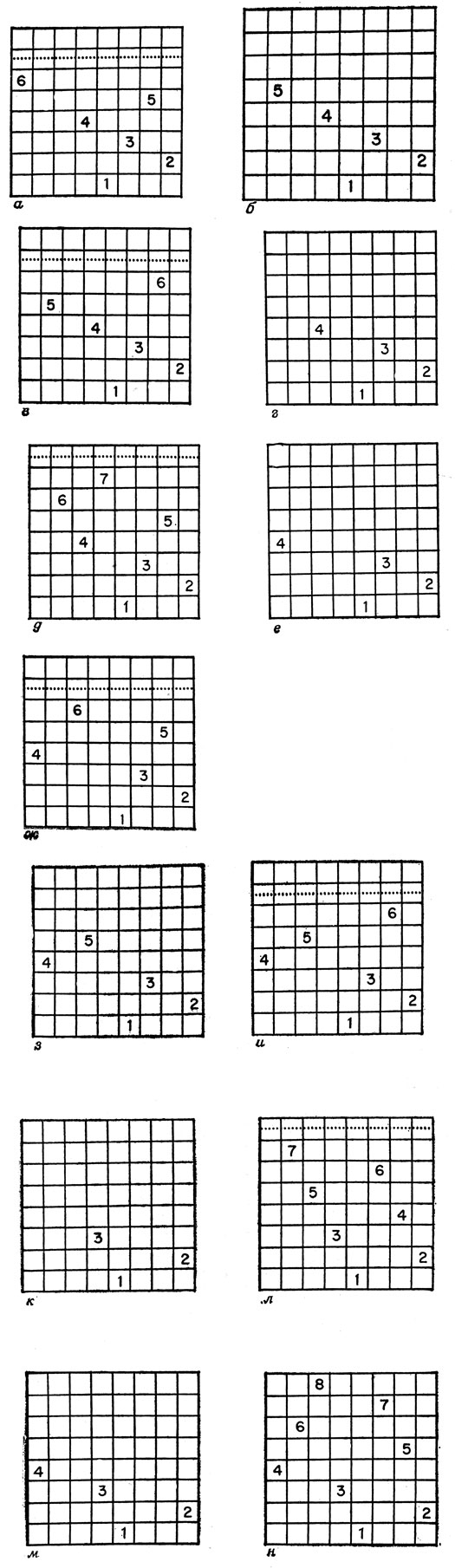
Рис. 69. Перебор в задаче о восьми ферзях

Однако уже на седьмой горизонтали все поля оказываются атакованными: мы попали в тупик. Поэтому мы возвращаемся на шаг назад и смотрим, можно ли найти другое место для шестого ферзя. Оказывается, расположение первых пяти ферзей на рис. 69, а полностью определяет расположение шестого ферзя, и поэтому необходимо сделать еще шаг назад и попробовать переставить пятого ферзя. Так мы приходим к рис. 69, б. Из него однозначно вытекает расположение рис. 69, в. Однако и в этом случае на седьмой горизонтали нет неатакованных полей, так что мы опять попали в тупик. Поскольку все возможности расположения пятого ферзя исчерпаны, мы должны вернуться назад и переставить четвертого ферзя.

Передвигая четвертого ферзя на ближайшее возможное поле четвертой горизонтали, мы приходим к позиции рис. 69, г, которая однозначно развивается в позицию рис. 69, д. Следующее и последнее расположение четвертого ферзя показано на рис. 69, г. В этом случае пятый ферзь может располагаться либо как на рис. 69, ж, либо как на рис. 69, з, который приводит к позиции на рис. 69, и. Итак, все рассмотренные позиции приводят к тупиковым ситуациям, а мы перебрали все случаи расположения ферзей при заданном расположении первых трех. Следовательно, надо сделать еще один шаг назад и передвинуть третьего ферзя в следующее возможное положение, показанное на рис. 69, к. Продолжая процесс последовательных шагов применительно к этой позиции, мы приходим к решению задачи о расстановке восьми ферзей, показанному на рис. 69, н.

Хотя подобное решение оказалось весьма трудоемким, время, которое оно займет, составляет ничтожную долю времени, за которое можно было бы рассмотреть хвыше четырех миллиардов расположений восьми ферзей. Более того, в разумные сроки методом перебора можно даже найти все решения нашей задачи. Читателю, который захочет испытать свои силы, подскажем, что существует лишь четыре принципиально разных возможных положения первого ферзя, расположенного на первой горизонтали. Решение, которое является, пожалуй, наиболее симметричным, изображено на рис. 70. Всего существует 92 решения задачи о расположении восьми ферзей, которые сводятся к 12 принципиально разным случаям - 12 ответов мы получим, если условимся не различать конфигурации, сводящиеся одна к другой поворотами и зеркальными отражениями шахматной доски. При попытках найти все решения задачи о восьми ферзях методом перебора следует учитывать наличие таких симметричных решений задачи. Так, перебрав все варианты решений, в которых первый ферзь стоит, как указано на рис. 69, н, в дальнейшем следует отбрасывать все решения, в которых хотя бы один из ферзей занимает клетку, симметричную той, которая отмечена единицей на рис. 69^*.

^* (Так, например, далее мы можем уже не анализировать случаи, когда один из ферзей стоит на клетке, отмеченной цифрой 4 на рис. 69, е - и (эта клетка получается из отмеченной цифрой 1 при повороте доски на 90°).)

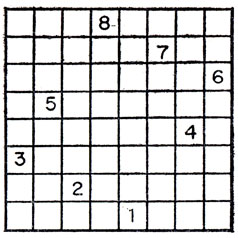
Рис. 70. Наиболее симметричное решение задачи о ферзях

Метод перебора не столь элегантен, как многие другие математические методы, однако он незаменим в решении комбинаторных задач. Более того, специфическое для этого метода решение задачи с помощью систематического продвижения вперед и назад до тех пор, пока либо решение не будет найдено, либо исчерпывающий анализ вариантов покажет, что оно не существует, делает метод перебора особенно удобным для составления на его основе программы работы ЭВМ. В электронных вычислительных машинах исходные данные (скажем, наши рисунки) задаются в числовой форме, после чего машина, следуя полученным инструкциям, манипулирует с числовыми данными вплоть до получения решения (которое, конечно, может быть и отрицательным, то есть состоять в доказательстве неразрешимости задачи). В отличие от человека машина, решая задачи, производит однообразные вычисления, которые кажутся нам столь скучными, с невообразимой быстротой. Но вместе с тем она не заметит способа упростить или улучшить решение, если этот способ не будет заранее учтен программистом, составляющим детальные инструкции для работы ЭВМ. Поэтому задача программиста заключается в составлении квалифицированных инструкций машине, в которых должно указываться, как осуществлять перебор, после чего утомительную работу по исследованию всех вариантов машина полностью возьмет на себя.