Модификации и обобщения

К только что рассмотренной нами тематике относится еще ряд весьма любопытных задач. Можно, скажем, попытаться найти минимальное число мономино, "вытесняющих" с шахматной доски размером 8×8 все 12 пентамино одновременно. Решение этой задачи приведено на рис. 63. Если рассматривать каждое из 12 фигурирующих на рисунке домино как два мономило, то мы получим 24 мономино, очевидно "вытесняющих" с доски любое пентамино; никакого же удовлетворяющего условию расположения на шахматной доске меньшего числа мономино, по-видимому, не существует.

Рис. 63. Для одновременного исключения всех 12 пентамино должны быть использованы 12 домино

Можно также задать себе вопрос: а какое наименьшее число мономино потребуется для того, чтобы "вытеснить" с доски во всяком случае 11 из 12 пентамино? Здесь ответ, вероятно, следует из рис. 64, где 21 мономино "вытесняют" все пентамино, за исключением W-пентамино.

Рис. 64. Чтобы исключить все пентамино, кроме W, надо взять 21 мономино

Другим примером такого рода задачи может служить вопрос о минимальном числе мономино, одновременно "вытесняющих" с доски каких-то два заданных пентамино. Так, например, мы уже выяснили выше (см. рис. 46), что для "вытеснения" с доски I-пентамино потребуется минимум 12 мономино. Примечательно, однако, что эти же 12 мономино можно расположить на шахматной доске таким образом, чтобы они одновременно "вытесняли" с доски и X-пентамино. Соответствующая конфигурация мономино изображена на рис. 65.

Рис. 65. 12 - минимальное число мономино, необходимых для исключения двух пентамино (X и I)

Вообще легко подсчитать, что, ставя задачи "вытеснения" с шахматной доски каждого из 12 пентамино в отдельности, а также всевозможных комбинаций из пар, троек и т. д. вплоть до всех 12 пентамино сразу, мы получим 4095 различных задач, которые предоставят вдумчивому читателю множество дополнительных упражнений.

Любопытно также поставить аналогичные вопросы для полимино меньшей площади - домино, тримино и т. д. Оптимальные размещения мономино изображены на рис. 66; доказательства этого мы предоставляем читателю. Заметьте только, что в большинстве случаев изображенные на рис. 66 расположения повторяют рис. 46. Это и не удивительно - ведь конфигурация мономино, "вытесняющая" с доски какое-то полимино, будет, естественно, "вытеснять" и любое полимино, получающееся из первого добавлением одного или нескольких квадратов. Любое же пентамино получается из какого-то одного или даже нескольких тетрамино, а уж тем более из тримино или домино.

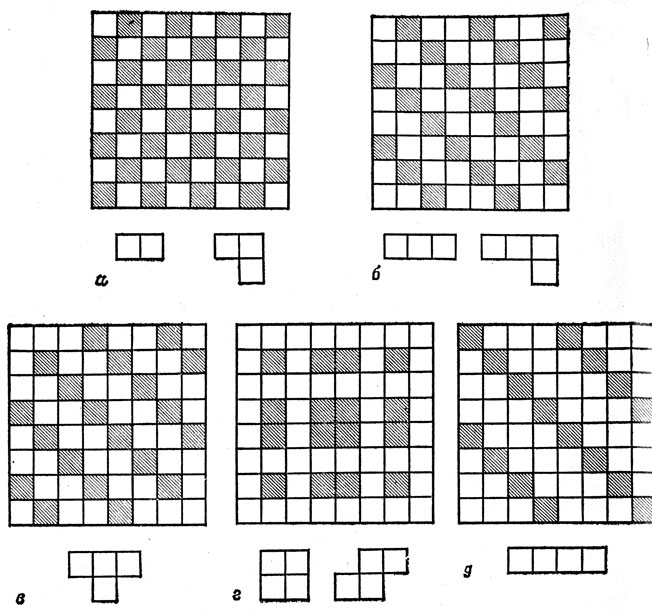
Рис. 66. Под 'досками' указаны минимальные числа мономино, необходимые для вытеснения каждого из полимино. а - 32 для домино и прямоугольного тримино; 6 - 21 для прямого тримино и L-тетрамино; в - 20 для Т-тетрамино; г - 16 для квадратного и косого тетрамино; д - 16 для прямого тетрамино

Следующим шагом в задаче о "вытеснении" пентамино будет переход от шахматной доски размером 8×8 ко всей (бесконечной!) плоскости. Здесь имеет смысл говорить о минимальной доле всей плоскости, занимаемой нашими мономино. Четыре покрытия плоскости, которые решают задачу для всех пентамино, изображены на рис. 67.

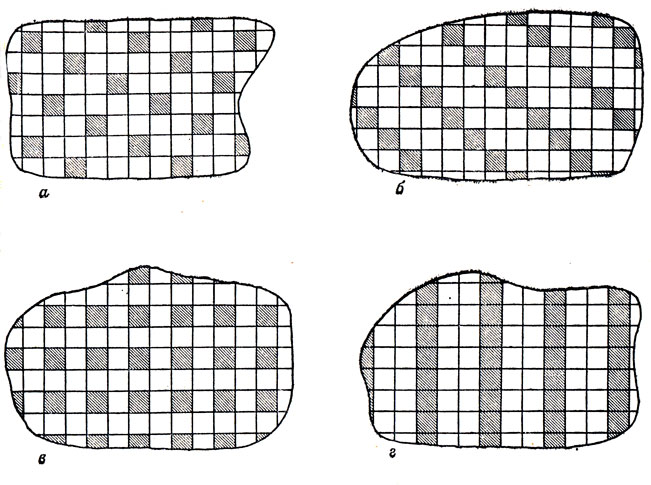
Рис. 67. Вытеснение пентамино с бесконечной доски. а - вытеснение X и I; б - вытеснение Т, U, Y и L; в - вытеснение W, F, Р и N; г - вытеснение V и Z

Из рис. 67, а видно, что, покрыв мономино всего лишь ¹/₅ часть всех клеток плоскости, мы можем "вытеснить" I- и X-пентамино. На рис. 67, б ¹/₄ клеток решает задачу для Т-, U-, Y- и L-пентамино; на рис. 67, в ¹/₄ клеток - для W-, F-, Р- и N-пентамино. Наконец, на рис. 67, д ¹/₃ всей плоскости, занятая мономино, "вытесняет" V- и Z-пентамино.

Решения ряда задач, приведенных в этой главе, в частности тех, что требовали "вытеснения" с шахматной доски отдельных пентамино, логически достаточно тонкие. В ряде других случаев изобретательность можно заменить простым перебором вариантов. Такой метод решения задач о полимино излагается в следующей главе.