Глава III. Где не размещаются пентамино?

Пентамино, вытесняемые мономино

Все рассмотренные до сих пор задачи заключались в складывании разнообразных фигур и узоров из пентамино и других полимино. Перейдем к задачам иного рода, в которых требуется указать, как можно "забаррикадировать" шахматную доску с тем, чтобы не дать возможности расположить на ней пентамино. Конкретно нас будет интересовать вопрос, скажем, о том, какое минимальное число мономино можно расположить на шахматной доске размером 8×8 так, чтобы после этого было бы невозможно разместить на доске хотя бы одно пентамино, причем не вообще пентамино, а конкретное пентамино - одно из 12 известных нам. Таким образом, мы получаем сразу 12 задач - по одной для каждого из пентамино. При этом "решить задачу" здесь означает, во-первых, привести пример расположения на шахматной доске нескольких мономино, "вытесняющих" заданное пентамино, и, во-вторых, доказать (тем или иным комбинаторным рассуждением или же просто соображениями очевидности), что меньшего числа мономино для этой цели не хватит.

Заметим прежде всего, что изображенные на рис. 44 три расположения мономино на шахматной доске сразу же доказывают, что 16 мономино для каждого из 12 пентамино будет достаточно. (Позже мы увидим, что для шести из 12 пентамино это число мономино - а именно 16 - будет и необходимо.) Четыре пентамино, указанные под каждым из изображенных на рис. 44 расположений, суть те, которые этими мономино "вытесняются". При этом легко заметить, что три пентамино (а именно Т, W и F) можно было бы подписать сразу под двумя из трех приведенных расположений мономино.

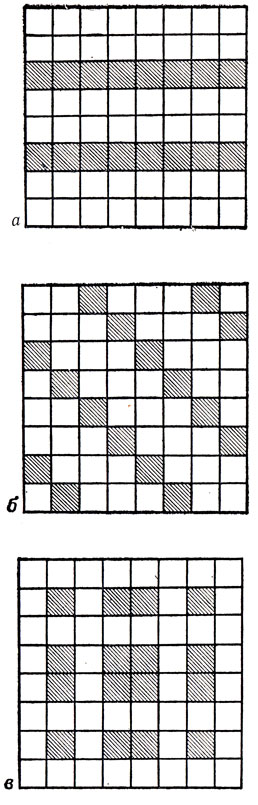
Рис. 44. Три рисунка, показывающие, что для исключения любого данного пентамино достаточно 16 мономино. а - исключение Т, U, V и Z; б - исключение U, Y, I и L; в - исключение W, F, Р и N

Для некоторых пентамино (скажем, для U-, V-, Y- или L-пентамино) уже этот первый шаг решения задачи вызывает обычно немало затруднений - придумать расположение на шахматной доске всего лишь 16 мономино, "вытесняющих" эти пентамино, не так-то просто. Если же все показанные на рис. 44 узоры найдены, то продвинуться дальше, а именно придумать изображенные на рис. 45 расположения, уже ничего не стоит. Из рис. 45, а видно, как можно "вытеснить" X-пентамино с помощью 12 мономино, а из рис. 45, б - как можно "вытеснить" I-пентамино с помощью 14 мономино. Однако, к огорчению тех, кто уже сумел продвинуться до этого места в решении поставленной задачи, ни та, ни другая конфигурация мономино не является наилучшей из возможных, то есть минимальной по числу использованных мономино. Наилучшие расположения мономино - девять расположений для 12 пентамино - изображены на рис. 46.

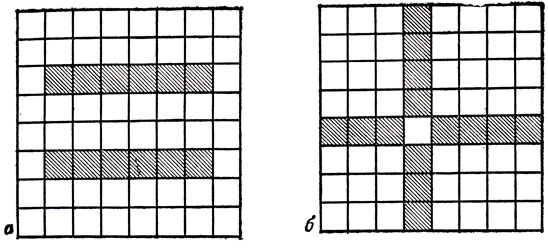
Рис. 45. а - для исключения X достаточно 12 мономино; б - для исключения I достаточно 14 мономино

Рис. 46. Сколько мономино достаточно для исключения с шахматной доски заданного пентамино? а - 10 для X; б - 12 для I; в - 14 для Т; г - 14 для Z; д - 14 для F; e - 15 для W; ж - 16 для V; з - 16 для Р или N; и - 16 для U, Y или L

Как показывает простая проверка, собранные на этом рисунке конфигурации с числом мономино от 10 до 16 удовлетворяют поставленному условию. Остается лишь показать, что указанные числа мономино и в самом деле минимальны. Все 12 доказательств минимальности основаны на сходных комбинаторных соображениях; рассмотрим их в порядке возрастания громоздкости рассуждений. (Четыре самых длинных доказательства мы предоставим читателям во всех деталях завершить самостоятельно.)

Наиболее простым является доказательство необходимости для I-пентамино. Для того чтобы убедиться в том, что менее чем 12 мономино нельзя вытеснить I-пентамино с шахматной доски, рассмотрим доску на рис. 47, где из нее выделены 12 прямоугольников размером 1×5 (каждый из них можно в точности покрыть одним I-пентамино). Если в конфигурации мономино на шахматной доске хоть один из наших 12 прямоугольников окажется не содержащим мономино, то можно с уверенностью сказать, что эта конфигурация не "вытесняет" I-пентамино, ибо мы сможем расположить I-пентамино на доске, покрывая им свободный от мономино прямоугольник. Поэтому любая "вытесняющая" I-пентамино конфигурация должна быть такова, что все 12 изображенных на рис. 47 прямоугольников размером 1×5 содержат минимум по одному мономино, и, значит, общее число мономино будет не меньше 12. Таким образом, для "вытеснения" I-пентамино с шахматной доски необходимо 12 мономино; к тому же, как видно из рис. 46, б, 12 мономино здесь будет и достаточно.

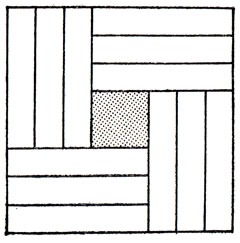
Рис. 47. Конструкция, используемая в доказательстве того, что для исключения I-пентамино необходимы по меньшей мере 12 мономино

К сожалению, ни для одного из пентамино, отличных от I-пентамино, нельзя, подобно рис. 47, разбить доску на k неперекрывающихся пентамино, где k равно минимальному числу мономино, требующихся для "вытеснения" нашего пентамино. Однако приведенное выше рассуждение несложно модифицировать, что позволит распространить его на случай тех шести пентамино, которые "вытесняются" с шахматной доски лишь с помощью 16 мономино, а именно на случай V-, Р-, N-, U-, Y- и L-пентамино.

Рассмотрим прежде всего Y-пентамино и разделим доску на 8 частей, как показано на рис. 48. Для того чтобы "вытеснить" Y-пентамино со всей шахматной доски, нужно во всяком случае "вытеснить" его с любого из восьми прямоугольников изображенного на рис. 48 разбиения. Но, как легко убедиться, одно мономино не может "вытеснить" пентамино с такого прямоугольника! В самом деле, в силу соображений симметрии существуют только два принципиально разных положения мономино внутри прямоугольника размером 2×4 - в углу прямоугольника и внутри него. Эти положения мономино отмечены крестиками на рис. 49, и в обоих случаях для Y-пентамино все еще остается место внутри прямоугольника. Следовательно, для каждого из наших прямоугольников размером 2×4 потребуется минимум по два мономино, а на все восемь прямоугольников - минимум 16 мономино. Как видно из рис. 46, и, 16 мономино достаточно для "вытеснения" Y-пентамино.

Рис. 48. Конструкция, используемая в доказательстве того, что для исключения Y-пентамино необходимы по меньшей мере 16 мономино

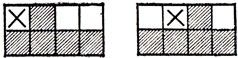
Рис. 49. Одного мономино недостаточно, чтобы исключить Y из прямоугольника 2×4

То же изображенное на рис. 48 разбиение позволяет решить задачу и в случае U-, L- или Р-пентамино. Отвечающие этим случаям модификации рис. 49 собраны на рис. 50.

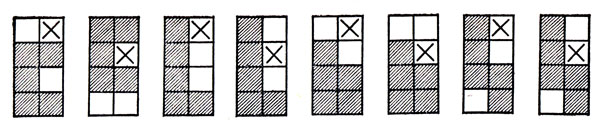
Рис. 50. Одного мономино недостаточно, чтобы исключить U, L, Р или N из прямоугольника 2×4

Итак, из перечисленных шести пентамино мы не рассмотрели лишь V-пентамино. Разобьем теперь доску на четверти - на четыре квадрата размером 4×4 (рис. 51). Чтобы доказать, что каждая четверть должна содержать минимум четыре мономино, будем исходить из противного: предположим, что мы как-то смогли "вытеснить" V-пентамино с квадрата размером 4×4 с помощью всего лишь трех мономино. При этом, очевидно, хотя бы одна строка (горизонтальный ряд клеток) и хотя бы один столбец (вертикальный ряд клеток) нашего квадрата окажутся свободными. Но пересекающиеся строка и столбец квадрата 4×4 всегда, как легко видеть, могут вместить V-пентамино: в этом можно убедиться, взглянув на рис. 51, где изображены три возможных случая взаимного расположения строки и столбца квадрата (внешняя строка и внешний столбец; внешняя строка и внутренний столбец; внутренняя строка и внутренний столбец). Таким образом, все наши четыре "четверти" шахматной доски должны содержать минимум по 4 мономино, откуда следует, что вся доска в целом должна содержать минимум 4×4 = 16 мономино.

Рис. 51. Не менее 16 мономино необходимы для исключения V

Следующее по сложности решение - для Т-пентамино. Теперь мы разобьем доску размером 8×8 на части так, как показано на рис. 52, а. Из пяти получающихся при этом частей центральная (8-клеточная) должна вмещать не меньше двух мономино, ибо из рис. 52, б - в с очевидностью следует, что одного мономино для "вытеснения" Т-пентамино с этой части шахматной доски недостаточно. Далее, чтобы доказать необходимость минимум трех мономино для каждой из четырех остальных получающихся при указанном разбиении доски частей (и, значит, необходимость минимум 2 + 3 × 4 = 14 мономино для всей доски в целом), предположим противное, а именно что для "вытеснения" Т-пентамино с такой части доски достаточно двух мономино. Разобьем нашу часть доски на две области так, как показано на рис. 52, г. Ясно, что одно из наших двух мономино должно будет заведомо принадлежать области, имеющей форму Т-пентамино; следовательно, на долю второй области также придется только одно мономино. Крестиком на рис. 52, г отмечено то единственное возможное положение мономино внутри указанной 9-клеточной фигуры, которое "вытесняет" с нее Т-пентамино. Но даже в случае расположения мономино на помеченном крестиком поле, как видно из рис. 53, независимо от положения другого мономино внутри второй области, на которые разбита наша 14-клеточная часть доски, мы все равно сможем отыскать в пределах всей этой части свободное место для Т-пентамино. Итак, для любой из четырех внешних фигур изображенного на рис. 52, а разбиения шахматной доски необходимо минимум три мономино, что и завершает решение задачи.

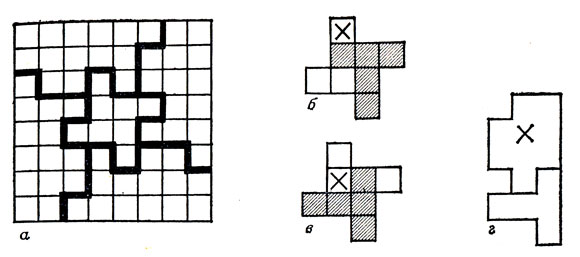
Рис. 52. Для исключения Т необходимо не менее 14 мономино

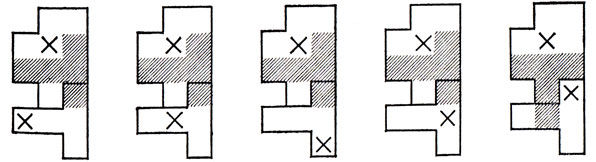
Рис. 53. Дальнейшие конструкции к задаче об исключении Т

Что же касается четырех оставшихся пентамино, к рассмотрению которых мы теперь перейдем, то все отвечающие им решения достаточно сложны и громоздки. Так, в случае W-пентамино приводящее к цели разбиение шахматной доски изображено на рис. 54. Нетрудно показать, что наименьшее количество мономино, "вытесняющих" W-пентамино с каждой из пяти частей представленного на этом рисунке разбиения доски, равно выписанному на этой части числу. Однако, к сожалению, сумма всех пяти полученных чисел равна 13, а точная оценка, которую нам требуется установить, - 15.

Рис. 54. Разбиение, используемое в задаче об исключении W

Предположим, что 13 мономино оказалось достаточно. Тогда при любых поворотах рис. 54 мономино, взятые в указанных на этом рисунке количествах, будут "вытеснять" W-пентамино. Наложение всех поворотов и зеркальных отражений доски приводит к изображенной на рис. 55 конфигурации частей. Каждая из четырех "угловых" областей потребует трех мономино; затененная же область в центре, поскольку она равна одной из "угловых" областей на рис. 54, потребует еще трех мономино. Следовательно, всего мы получим 15 мономино. Итак, начав с предположения о том, что 13 мономино здесь достаточно, мы затем опровергли это предположение, убедившись, что на самом деле 13 мономино не хватит. Дальнейший ход рассуждений убеждает нас, что в действительности необходимо 15 мономино. Из рис. 46, е следует, что этого числа мономино будет и достаточно.

Рис. 55. Сводка ограничений, наложенных вращениями и зеркальными отражениями рис. 54

Доказательства для оставшихся трех пентамино (X, F и Z) близки к приведенному для W-пентамино. Отправным пунктом всякий раз служит простая картинка, пусть даже она дает число мономино, на два меньшее необходимого нам. Примером в данном случае может послужить рис. 56. Из рис. 56, а видно, что восемь мономино необходимо для "вытеснения" Х-пентамино; из рис. 56, б - что 12 мономино необходимо для "вытеснения" F-пентамино; из рис. 56, в - что 12 мономино необходимо для "вытеснения" Z-пентамино.

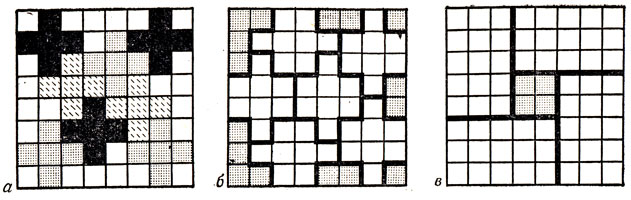
Рис. 56. Разбиение, показывающее мономино, необходимые для исключения X (a); F (б); Z (в)

Чтобы убедиться в необходимости девяти мономино в случае Х-пентамино, обратимся к рис. 57, а. Если бы восьми мономино было достаточно, они должны были бы принадлежать восьми X-областям рис. 57, а, причем независимо от того, как мы поворачиваем и зеркально отражаем доску с этим узором. Отсюда следует, что все мономино будут принадлежать незатененным областям на рис. 57, б. Но большая центральная затененная область на рисунке должна содержать во всяком случае два мономино - иначе с нее нельзя будет "вытеснить" Х-пентамино. Это рассуждение и опровергает предположение о достаточности восьми мономино. И здесь дальнейшее развитие тех же идей приводит к числу 10.

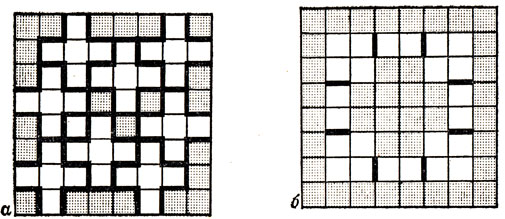
Рис. 57. Конструкция, показывающая, что восьми мономино недостаточно для исключения X

Обращаясь к F-пентамино, рассмотрим рис. 58, а. На каждой из имеющихся здесь областей указано число мономино, необходимое для "вытеснения" с нее F-пентамино. Чтобы доказать это для области, помеченной числом 3, рассмотрим ее разбиение, изображенное на рис. 58, б. Предположим, что двух мономино достаточно. Ясно, что одно из них должно принадлежать F-области. Единственное возможное положение второго мономино внутри другой области, "вытесняющее" из этой области F-пентамино, - это то, которое на рис. 58, б помечено крестиком. Однако, комбинируя любое поле F-области с помеченным крестиком полем, мы каждый раз оставляем место для F-пентамино.

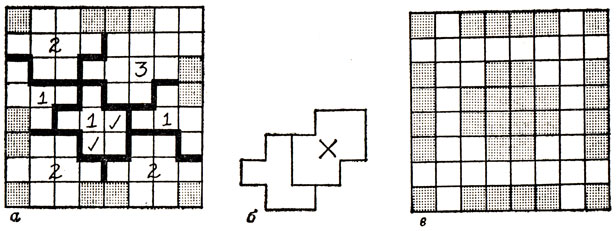
Рис. 58. Конструкция, используемая для доказательства недостаточности 12 мономино для исключения F

Область, помеченная на рис. 58, а двумя галочками, вмещает F-пентамино даже после того, как мы покроем мономино одно из помеченных галочками полей. Подвергнув рис. 58, а всевозможным поворотам и зеркальным отражениям, мы заключим, что все 12 мономино (если они "вытесняют" F-пентамино) должны принадлежать незатененным на рис. 58, в частям доски. Но еще минимум два мономино понадобятся для центральной затененной области, что и доказывает недостаточность 12 мономино. Дальнейшие рассмотрения позволяют установить, что в этом случае 14 мономино будет необходимо и достаточно.

Нам осталось рассмотреть лишь случай Z-пентамино. На рис. 59, а все четыре "угла", как легко показать, должны содержать минимум по три мономино. Это можно строго доказать с помощью все того же приема: выделяя из каждого "угла" по Z-области и убеждаясь, что вне ее придется поместить более чем одно мономино.

Рис. 59. Конструкция, используемая для доказательства недостаточности 12 мономино для исключения Z

Поворачивая и зеркально отражая рис. 59, а всевозможными способами, мы убедимся, что если для "вытеснения" Z-пентамино достаточно 12 мономино, то все они должны принадлежать незатененным на рис. 59, б частям доски. Вместе с тем затененная на том же рисунке часть доски одновременно может содержать четыре неперекрывающихся пентамино. Отсюда следует, что 13 мономино во всяком случае необходимы.

Мы наметим сейчас доказательство того, что на самом деле для "вытеснения" Z-пентамино с шахматной доски необходимо (и достаточно) не 13, а 14 мономино. Во-первых, разобьем доску на четыре одинаковые части, как показано на рис. 59, в. Предположим, что 13 мономино достаточно для "вытеснения" Z-пентамино (что это число необходимо, мы уже убедились). В гипотетической конфигурации из 13 мономино минимум четыре мономино будут принадлежать одной из наших четырех областей (ибо четыре числа, каждое из которых не больше трех, никак не могут дать в сумме 13). Повернем доску так, чтобы та ее четверть, которая содержит четыре мономино, оказалась вверху слева; оставшуюся часть доски, содержащую не более девяти мономино, разобьем на два куска так, как показано на рис. 60. Поскольку из заштрихованной нижней фигуры нельзя "вытеснить" Z-пентамино с помощью меньше чем трех мономино, то вторая - большая незаштрихованная - часть доски будет содержать их не больше шести. Итак, остается показать, что шести мономино для большей фигуры недостаточно.

Pис. 60. Конструкция, используемая для получения противоречия утверждению о достаточности 13 мономино для исключения Z

Последнее доказательство можно провести методом "от противного". Предположим, что с помощью шести мономино можно "вытеснить" Z-пентамино из рассматриваемой 34-клеточной фигуры. При этом все шесть мономино должны принадлежать незаштрихованным на рис. 61, а частям доски, ибо каждая из них требует минимум по три мономино. Точно так же показывается, что все шесть мономино принадлежат двум незаштрихованным на рис. 61, б частям доски, и аналогично для рис. 61, в-д. Совмещая затем рис. 61, а-д между собой, мы придем к выводу, что шесть мономино, "вытесняющие" Z-пентамино со всей 34-клеточной фигуры, размещаются по три в каждой из незакрашенных на рис. 61, е частей доски.

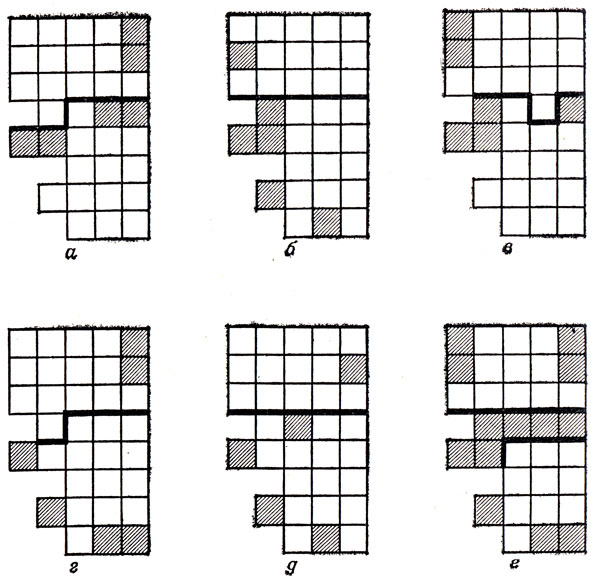
Рис. 61. Дальнейшие конструкции к задаче об исключении Z

Рассмотрим верхнюю часть рис. 61, е. Три мономино, расположенные внутри незаштрихованной области рис. 62, а, должны "вытеснять" Z-пентамино со всей изображенной на этом рисунке 21-клеточной фигуры. Нетрудно видеть, что единственный возможный способ осуществить это показан на рис. 62, б.

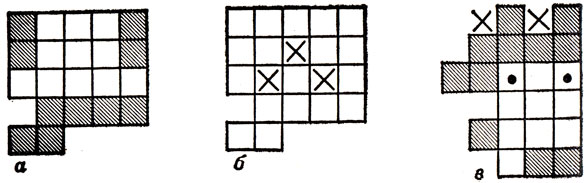
Рис. 62. Последняя конструкция к задаче об исключении Z

Нижняя часть рис. 61, е изображена на рис. 62, в; две верхние заштрихованные клетки на этом рисунке заимствованы из рис. 62, б. Три мономино в незаштрихованной части должны "вытеснить" из нее Z-пентамино. Две помеченные точками клетки заведомо должны содержать мономино, ибо их можно покрыть Z-пентамино, все остальные клетки которого будут целиком принадлежать заштрихованной части рис. 62, в. Оставшегося же одного мономино будет явно недостаточно, чтобы полностью "вытеснить" Z-пентамино

Тем самым мы пришли к требуемому противоречию: 13 мономино недостаточно для "вытеснения" Z-пентамино с шахматной доски. Здесь необходимо минимум 14 мономино. Как видно из рис. 46, г, этого числа будет и достаточно.