Задачи о кладке

Роберт И. Джуэтт, будучи еще аспирантом Орегонского университета, предложил весьма любопытную задачу: можно ли сложить из двух или более костей домино прямоугольнику в котором не найдется ни одной прямой, проходящей по краям костей домино и соединяющей две его противоположные стороны (то есть разбивающей наш прямоугольник на два меньших)? Например, на рис. 38 такая линия есть:

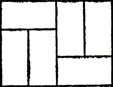
Рис. 38. Прямоугольник из домино, содержащий рассекающую линию

это вертикальная прямая посредине прямоугольника. Если вместо домино представить себе кирпичи, то наличие такой линии будет свидетельствовать о непрочности кладки. Таким образом, задача Джуэтта сводится к отысканию "прочной" кладки без подобных "швов".

Многие из тех, кто брался за эту задачу, вскоре сдались, будучи уверены, что она неразрешима. На самом же деле решений существует бесконечно много - правда, даже в тех из них, которые содержат наименьшее возможное число костей домино, этих костей участвует 15 и составляют они прямоугольник размером 5×6. Два совсем разных покрытия такого прямоугольника, удовлетворяющие требуемым условиям, указаны на рис. 39.

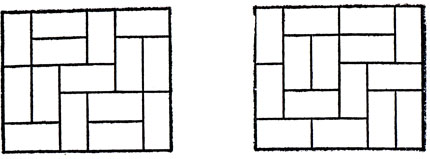
Рис. 39. Два 'прочных' прямоугольника 5×6

Легко показать, что наименьшая ширина "прочного" прямоугольника должна превышать четыре клетки. (Случай прямоугольника шириной в две клетки совершенно очевиден: достаточно постараться покрыть две клетки прямоугольника, примыкающие к его наименьшей стороне, - если эти две клетки будут покрыты одним домино, то мы сразу же получим "опасный шов", а если они будут покрыты разными костями домино, то, как легко видеть, мы все равно получим такую линию. Читателю предлагается самому рассмотреть случаи прямоугольников шириной в три и четыре клетки.) И так как к тому же 5×5 = 25 - нечетное число, а любое количество костей домино всегда, очевидно, покроет четное число клеток, то прямоугольник размером 5×6 действительно наименьший из возможных.

Прямоугольник размером 5×6 легко превратить в прочную шахматную доску размером 8×8. Как это сделать, подскажет вам рис. 40.

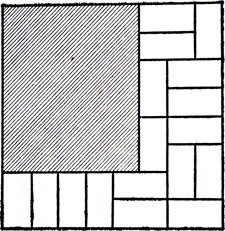
Рис. 40. Как из 'прочного' прямоугольника 5×6 получить 'прочную' доску 8×8

Как ни удивительно, "прочих" прямоугольников размером 6x6 не существует. Этот факт имеет замечательное доказательство. Представим себе, что прямоугольник размером 6×6 мы замостили 18 костями домино (число костей должно равняться половине числа квадратов!). Пример такого покрытия ("непрочного") изображен на рис. 41, где жирные линии разбивают прямоугольник на меньшие прямоугольники. Сетка, делящая наш прямоугольник на клетки, состоит, очевидно, из 10 линий (5 вертикальных и 5 горизонтальных); прямоугольник будет "прочным", если каждая из этих линий пересекает хотя бы одно домино.

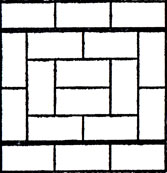
Рис. 41. 'Непрочное' покрытие прямоугольника 6×6

Покажем теперь, что в нашем прямоугольнике размером 6×6 каждая прямая сетки будет заведомо пересекать четное число костей. Возьмем, к примеру, любую вертикальную прямую сетки. Площадь (то есть число четных квадратов) слева от нее четная: она равна 6, 12, 18, 24 или 30 квадратам. Ясно, что площадь, занимаемая костями домино, которые целиком лежат слева от нашей прямой, тоже четная - ведь каждое домино покрывает две клетки. Отсюда будет четной и площадь, которую занимают слева половинки разрезаемых этой прямой домино, ибо она равна разности двух четных чисел: всей площади слева и площади, покрытой лежащими слева неразрезанными домино. А так как разрезаемые нашей прямой кости домино имеют слева от нее всего по одной клетке, то мы и получаем, что этих костей - четное число.

Сетка в квадрате 6×6 содержит 10 прямых. Если же наш прямоугольник 6×6 "прочный", то, как следует из приведенного выше доказательства, каждая прямая будет пересекать хотя бы два домино. Но так как кость домино нельзя пересечь более чем одной линией сетки, то вся сетка разрезает не менее 20 костей домино. В прямоугольнике же размером 6×6 расположено всего лишь 18 костей домино!

Точно так же можно показать, что при "прочном" замощении прямоугольника размером 6×8 любая линия сетки обязательно будет пересекать ровно два домино. Такое покрытие прямоугольника 6×8 изображено на рис. 42.

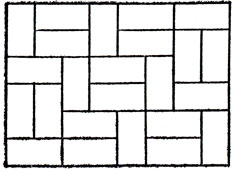
Рис. 42. 'Прочное' покрытие прямоугольника 6×8, в котором каждая рассекающая линия пересекает в точности два домино

В общем случае ответ на поставленный Джуэттом вопрос гласит: "прочное" покрытие прямоугольника несколькими домино существует, если длина и ширина этого прямоугольника больше четырех, а площадь его четная; единственное исключение - прямоугольник размером 6×6.

Очень просто получать покрытие прямоугольников большего размера увеличением длины или ширины на две клетки. Рис. 43 иллюстрирует случай, когда прямоугольник размером 5×6 превращен в прямоугольник размером 5×8. Вообще при увеличении длины покрываемого прямоугольника на две клетки вправо или влево возле каждого примыкающего к стороне горизонтально положенного домино нужно расположить еще одно, все вертикальные домино сместить до новой границы, а освободившиеся при этом клетки заполнить горизонтальными домино.

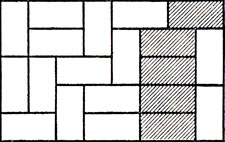
Рис. 43. Увеличение длины (или ширины) 'прочного' прямоугольника на 2

Любопытно, что получится, если за "кирпичи" принять не домино, а прямые тримино? Предлагаем этот вопрос читателю в качестве упражнения. В частности, каковы будут при этом размеры наименьшего "прочного" прямоугольника?