Задачи с тетрамино

В отличие от пентамино из пяти различных тетрамино прямоугольник сложить нельзя. Мы докажем это, раскрасив в шахматном порядке всевозможные прямоугольники площадью в 20 клеток. Их всего два: прямоугольник 4×5 и прямоугольник 2×10 (рис. 35). Четыре из наших тетрамино покрывают две черные и две белые клетки, пятое же - Т-тетрамино - всегда покроет три клетки одного цвета и одну - другого (рис. 36). Поэтому все пять тетрамино покроют нечетное число клеток каждого цвета, а оба изображенных на рис. 35 прямоугольника, как легко видеть, содержат по 10 белых и 10 черных клеток, то есть четное число тех и других.

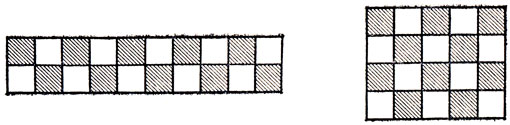
Рис. 35. Шахматная раскраска прямоугольников 2×10 и 4×5

Рис. 36. Четыре 'уравновешенных' и крайнее правое - 'неуравновешенное' тетрамино

В то же время среди 12 пентамино есть несколько таких, которыми вместе с пятью тетрамино можно покрыть квадрат размером 5×5. Два примера приведены на рис. 37. Попробуйте ответить на вопрос: сколько разных пентамино подойдут для этой цели?

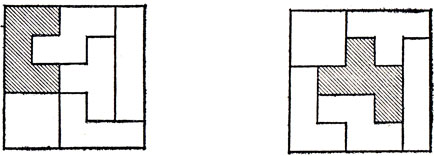
Рис. 37. Тетрамино можно комбинировать с одним пентамино для составления квадрата 5×5