Фигуры из пентамино

Новый класс игр с пентамино, который мы сейчас рассмотрим, можно охарактеризовать как задачи "совмещения" фигур, то есть задачи о складывании из пентамино двух или более равных между собой фигур. Приведем несколько примеров:

1. Попробуйте составить из 12 различных пентамино два одинаковых прямоугольника размером 5×6 (на каждый будет затрачено по 6 пентамино). На рис. 21 изображены отвечающие этим прямоугольникам наборы пентамино, причем любопытно, что приведенное разбиение наших фигур на два набора по шесть пентамино - единственно возможное. Впрочем, из этого не следует, что задача имеет единственное решение. В самом деле, для изображенного на рисунке справа набора фигур мы можем по-разному соединить F- и N-пентамино, получив при этом одну и ту же фигуру (как?).

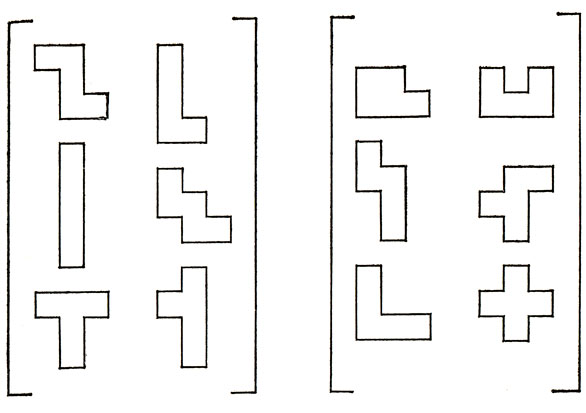
Рис. 21. Два набора по 6 пентамино, из которых можно составить прямоугольники 5×6

Заметим, между прочим, что решение этой задачи одновременно служит решением задачи о покрытии 12 пентамино прямоугольников размерами 5×12 и 6×10. Для того чтобы убедиться в этом, достаточно приложить друг к другу двумя способами наши прямоугольники размером 5×6.

2. Найдите такое покрытие 12 разными пентамино шахматной доски размером 8×8 с отверстием размером 2×2 в центре доски, чтобы доску можно было разбить на две одинаковые части, каждая из которых покрыта шестью пентамино. Три типичных решения этой задачи приведены на рис. 22.

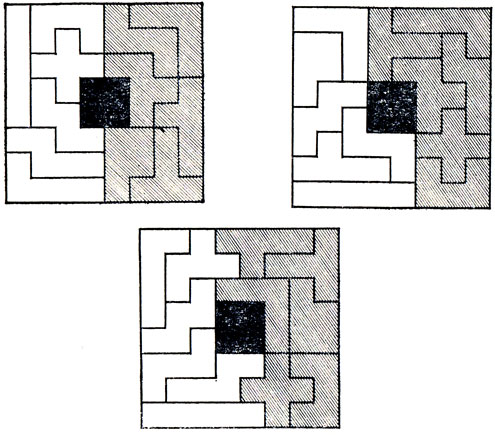
Рис. 22. Типичное решение задачи о покрытии шахматной доски 8×8 с центральной 'дыркой' 2×2, причем покрытие разбивается на две конгруэнтные части

3. Разбейте 12 пентамино на три группы по четыре фигуры в каждой так, чтобы при этом существовала 20-клеточная "доска", которую можно покрыть четырьмя пентамино, образующими любую из групп. Решение, изображенное на рис. 23, вовсе не единственное; читатель может попытаться найти свое решение.

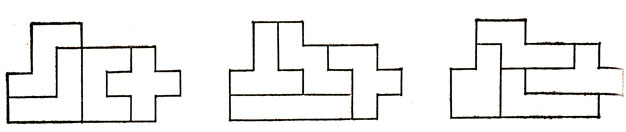
Рис 23. Решение задачи о трех конгруэнтных группах

4. Снова разбейте наши 12 пентамино на три группы по четыре пентамино; каждую группу в свою очередь разбейте на пары пентамино и придумайте три 10-клеточные "доски" (свою для каждой группы), покрываемые любой из входящих в соответствующую группу пар полимино. Одно из решений приведено на рис. 24. Постарайтесь найти другие решения, в частности такие, где ни одна из трех "досок" не имеет отверстий (подобные решения существуют).

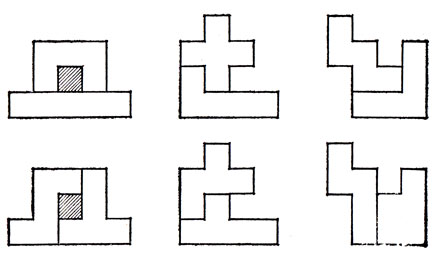
Рис. 24. Решение задачи о трех конгруэнтных парах

5. Еще раз разбейте 12 пентамино на три группы по четыре полимино в каждой. Если теперь ко всем наборам добавить по мономино, можно попытаться сложить из них три прямоугольника размером 3×7. Решение задачи показано на рис. 25. Известно, что других решений нет, если не считать того, что в самом левом прямоугольнике можно переложить мономино и Y-пентамино таким образом, чтобы в целом они составили ту же фигуру.

Рис. 25. Решение задачи о покрытии трех прямоугольников 3×7

Доказательство единственности решения последней задачи было подсказано инженером К. С. Лоренсом из компании "Аэроспейс Корпорейшн" (Лос-Анджелес) Прежде всего, нетрудно видеть, что Х-пентамино необходимо скомбинировать с U-пентамино, приложив их друг к другу так, как показано на рис. 26. Завершая первый прямоугольник, мы, очевидно, уже не сможем воспользоваться ни F-, ни W-пентамино. Легко заметить также, что последние две фигуры заведомо должны принадлежать разным прямоугольникам размером 3×7; иначе говоря, из трех наших прямоугольников размером 3×7 один будет содержать Х- и U-пентамино, другой - W-пентамино и, наконец, третий - F-пентамино. Мы предоставляем читателю возможность самостоятельно закончить решение задачи и с помощью несложного, хотя и довольно скучного разбора всех возможных оставшихся вариантов расположения фигур показать, что решение, изображенное на рис. 25, в самом деле является единственным.

Рис. 26. Единственно возможное положение Х-пентамино в прямоугольнике 3×7

6. Разложите наши 12 пентамино в четыре группы по три фигуры в каждой и придумайте такую 15-клеточную "доску", чтобы ее можно было покрыть всеми пентамино любой из групп.

Эта задача до сих пор не решена, но вместе с тем и не доказано, что такой "доски" не существует.

7. Вырежьте из шахматной доски фигуру наименьшей возможной площади, состоящую из некоторого числа примыкающих друг к другу клеток доски, так, чтобы на этой фигуре разместилось любое пентамино.

Минимальная площадь такой фигуры - 9 квадратов (клеток); два 9-клеточных решения задачи приведены на рис. 27. В самом деле, нетрудно проверить, что любое пентамино уместится на каждой из изображенных на рисунке "досок". С другой стороны, можно доказать, что наименьшая возможная площадь требуемой фигуры есть площадь в 9 квадратов. Действительно, если бы существовала менее чем 9-клеточная фигура, удовлетворяющая требуемым условиям, то, размещая на ней I-, Х- и V-пентамино, мы совместили бы их так, чтобы они вместе покрывали площадь не более чем 8 клеток. Ясно, что I- и Х-пентамино совместятся при этом по трем клеткам: в противном случае мы либо сразу же получим фигуру из 9 клеток, либо (если центральная клетка Х-пентамино совпадет с крайней клеткой I-пентамино) придем к фигуре из 9 клеток - если потребуем, чтобы на этой фигуре можно было бы разместить и V-пентамино. Но этому условию отвечают всего две изображенные на рис. 28 конфигурации из 8 клеток, такие, что и V-пентамино размещается на рассматриваемой "доске". Однако легко видеть, что на обеих "досках" не умещается, например, U-пентамино; для того чтобы обеспечить размещение на "доске" также и U-пентамино, потребуется увеличить любую из изображенных на рис. 28 фигур еще минимум на одну клетку. Таким образом, площади в 8 клеток для решения задачи будет не хватать, в то время как 9-клеточные фигуры, удовлетворяющие условию задачи, как мы видели выше, существуют.

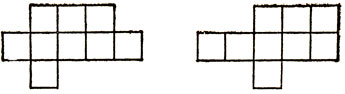
Рис. 27. Минимальные области, в которые можно поместить любое из 12 пентамино

Рис. 28. Минимальные области для I-, Х- и V-пентамино

Несколько лет назад к решению разнообразных задач о полимино были привлечены современные электронные вычислительные машины. Так, в сообщении известного американского специалиста по математической логике Дана Стюарта Скотта, профессора Стэнфордского университета (см. библиографию в конце книги), говорилось о двух задачах, решенных с помощью ЭВМ Стэнфордского университета MANIAC. Первая из них, уже знакомая нам, состояла в складывании из 12 разных пентамино прямоугольника размером 3×20. Выяснилось, что два ее решения, указанные на стр. 24, являются единственно возможными. Вторая задача заключалась в перечислении всех возможных покрытий 12 различными пентамино шахматной доски размером 8×8, в центре которой вырезан квадрат размером 2×2 (квадратное тетрамино). Оказалось, что последняя задача имеет 65 разных (то есть не получающихся друг из друга поворотами и отражениями доски) решений.

При составлении программы Д. Скотт воспользовался очень простой и остроумной идеей, которая заключалась в следующем: Х-пентамино можно расположить на шахматной доске лишь тремя существенно различными способами, показанными на рис. 29; Электронная вычислительная машина MANIAC нашла 20 решений для первого расположения Х-пентамино, 19 - для второго и 26 - для третьего расположения. Три из наиболее интересных решений, входящих в число этих 65, приведены на рис. 30, а на рис. 31 показаны три невозможные ситуации - они невозможны просто потому, что их нет в списке Скотта.

Рис. 29. Три возможных положения Х-пентамино на шахматной доске 8×8 с удаленным центральным квадратом 2×2

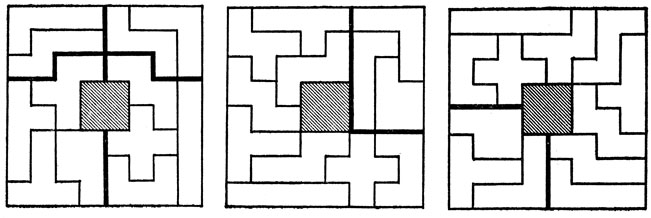
Рис. 30. Три интересных решения задачи о покрытии доски 8×8 с удаленным центральным квадратом 2×2

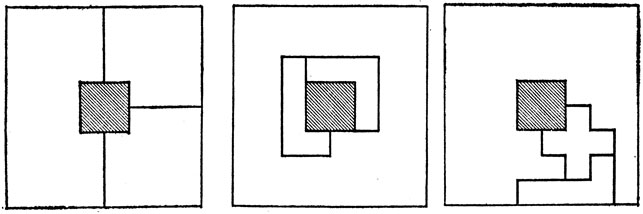
Рис. 31. Невозможные покрытия полимино шахматной доски 8×8

Профессор Манчестерского университета С. Б. Хэзелгроув, английский астроном, известный также своими результатами по теории чисел, не так давно с помощью ЭВМ подсчитал число всевозможных способов сложения из всех 12 пентамино прямоугольника размером 6×10. Вот его результат: не считая поворотов и отражений шахматной доски, ЭВМ нашла 2339 принципиально разных решений! Вместе с тем Хэзелгроув проверил и подтвердил два названных выше результата Дана Скотта.

В заключение приведем еще три несомненно заслуживающие внимания задачи, относящиеся к составлению фигур из пентамино:

1. Покройте "64-клеточную пирамиду", изображенную на рис. 32, 12 разными пентамино и квадратным тетрамино (впрочем, последнее можно заменить любым другим тетрамино). Одно из решений приведено на рис. 32.

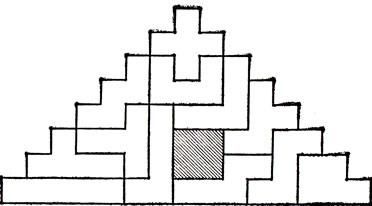
Рис. 32. 'Треугольник' из 64 квадратов

2. Покройте 12 пентамино вытянутый крест, изображенный на рис. 33.

Рис. 33. Вытянутый крест, составленный из пентамино

3. Профессору Р. М. Робинсону (который также впервые указал "зубчатый квадрат", приведенный в гл. VI) принадлежит очень простое доказательство того, что 60-клеточную фигуру, показанную на рис. 34, нельзя покрыть 12 разными пентамино. В самом деле, с краев эта фигура ограничена 22 клетками (считая и четыре угловые), а если сосчитать, сколько квадратов каждого из 12 пентамино может находиться на краю нашей фигуры, то в сумме мы получим всего лишь 21 клетку - на единицу меньше, чем требуется:

Т-пентамино - 1; W-пентамино - 3; Z-пентамино - 1; L-пентамино - 1;
U-пентамино - 1; Х-пентамино - 3; F-пентамино - 3; Р-пентамино - 2;
V-пентамино - 1; Y-пентамино - 2; 1-пентамино - 1; N-пентамино - 2 
 Итого: 21 клетка.

Рис. 34. Зубчатая область из 60 квадратов, предложенная Р. М. Робинсоном

Рассуждения такого рода, где отдельно рассматриваются внутренние и "граничные" клетки доски, весьма полезны при складывании "зигзагообразных" фигур.

Другие любопытные головоломки с пентамино будут рассматриваться в гл. VI.