Пентамино

Полимино, покрывающие пять клеток шахматной доски, называются пентамино. Существует 12 видов пентамино, которые можно обозначить прописными латинскими буквами, как указано на рис. 10. В качестве приема, позволяющего легко запомнить эти наименования, укажем, что соответствующие буквы составляют конец латинского алфавита (TUVWXYZ) и входят в имя FILiPiNo^*. Поскольку всего имеется 12 разных пентамино и каждая из этих фигур покрывает пять клеток доски, то вместе они покрывают 60 клеток.

^* (Филиппино - уменьшительная форма итальянского имени Филиппо (Филипп). В оригинале книги фигурирует английское слово Filipino - филиппинец.)

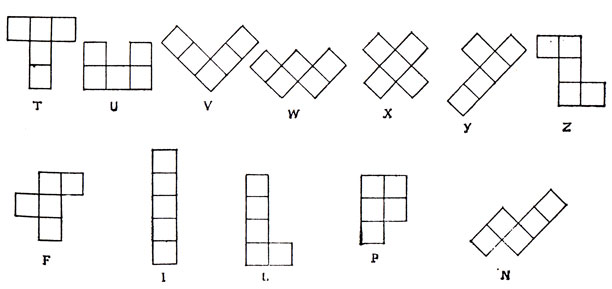
Рис. 10. Двенадцать пентамино

Возможно самыми разнообразными способами разместить на доске размером 8×8 все 12 пентамино, оставляя непокрытыми четыре поля доски. Много красивых расположений возникает при симметричном выборе этих клеток; три из них изображены на рис. 11.

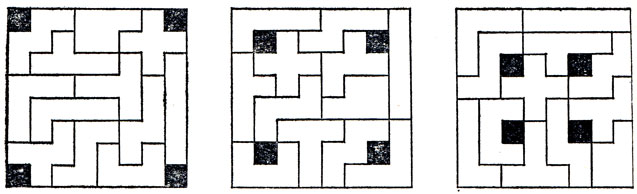
Рис. 11. Три способа укладки всех 12 пентамино на шахматной доске

Другая естественная постановка задачи заключается в требовании, чтобы четыре незанятые клетки составляли на доске квадрат размером 2×2, то есть чтобы их можно было покрыть квадратным тетрамино. (Самыми интересными здесь являются расположения тетрамино в центре или в углу доски.) По поводу расположения этого квадратного тетрамино можно высказать следующую замечательную теорему: независимо от того, где на шахматной доске расположено квадратное тетрамино, оставшиеся 60 клеток можно покрыть 12 разными пентамино.

Доказательство этой теоремы мы разобьем на три этапа. Заметим прежде всего, что очень большое, на первый взгляд, число возможных положений квадратного тетрамино на шахматной доске, а именно 49 (см. рис. 12, где точками отмечены расположения центра квадрата), соображениями симметрии сводится всего к 10 существенно разным расположениям, указанным на рис. 13.

Рис. 12. 49 возможных положений центра квадратного тетрамино

Рис. 13. 10 несимметричных положений центра квадратного тетрамино

Далее сложим из квадратного тетрамино и V-пентамино квадрат размером 3×3, как показано на рис. 14. После этого три покрытия шахматной доски, изображенные на рис. 15, уже завершают доказательство - ведь, как легко видеть, любое из 10 фигурирующих на рис. 13 расположений тетрамино можно получить, выбрав одно из указанных трех покрытий и располагая нужным образом внутри затененного квадрата размером 3×3 наше квадратное тетрамино.

Рис. 14. Покрытие квадрата 3×3 V-пентамино и квадратным тетрамино

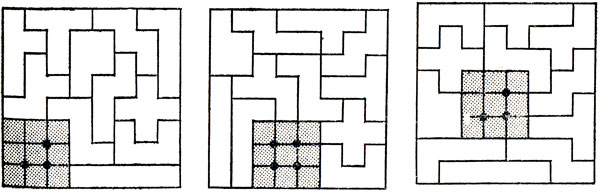
Рис. 15. Три укладки, показывающие, что удаление любого квадрата 2×2 из шахматной доски не препятствует покрытию оставшейся части доски 12 различными пентамино

Любопытен и следующий вопрос, относящийся к пентамино: каким наименьшим числом пентамино можно "заминировать" шахматную доску? Под "заминированием" доски здесь понимается такое расположение на ней нескольких пентамино, что ни одно из оставшихся пентамино поместить на шахматной доске более нельзя. Это наименьшее число пентамино, необходимое для "заминирования" шахматной доски, - 5. Одно из возможных решений задачи показано на рис. 16.

Рис. 16. Пять пентамино, перекрывающих шахматную доску

Помимо перечисленных, существует и множество других красивых задач с 12 пентамино; читатель может, например, заняться покрытием прямоугольников размерами 6×10, 5×12, 4×15 или 3×20. Здесь сложнейшей, пожалуй, является задача о прямоугольнике размером 3×20; ее решение показано на рис. 17, причем известно, что это решение единственно возможное, если отвлечься от того, что заштрихованную часть прямоугольника можно повернуть на 180°.

Рис. 17. Укладка 12 пентамино в форме прямоугольника 3×20

Р. М. Робинсон, профессор математики Калифорнийского университета в Беркли, предложил изящную задачу, получившую название задачи об утроении: выбрав одно из 12 пентамино, нужно построить из каких-то 9 остальных пентамино фигуру, подобную выбранной. Эта фигура будет, очевидно, втрое выше и втрое шире исходной. Задача об утроении допускает много красивых решений; два таких решения - для V-пентамино и для Х-пентамино - изображены на рис. 18. Задача об утроении, как ни странно, решается для любого из 12 пентамино, и читатель может попробовать самостоятельно "утроить" остальные 10 пентамино.

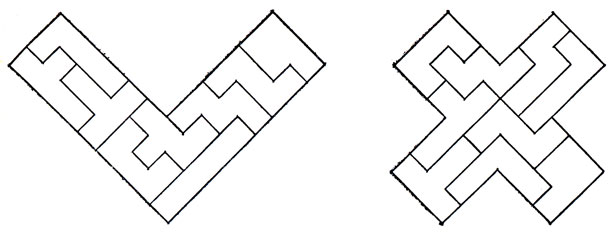
Рис. 18. Утроение V-пентамино и Х-пентамино

Пентамино - это не только задачи. Их размещения на шахматной доске размером 8×8 можно рассматривать и как увлекательную игру. Несколько (двое или больше) игроков поочередно выбирают любое из 12 пентамино и располагают его на свободных клетках шахматной доски. Проигрывает тот, кто первым не сможет разместить на доске ни одного из оставшихся пентамино. Если же все 12 пентамино удалось разместить на доске, то выигрывает ходивший последним. Эта игра наверняка будет продолжаться не менее 5 и не более 12 ходов и заведомо не может закончиться вничью; в начале партии имеется даже больше разнообразных "ходов", чем у шахмат. Игра, бесспорно, заинтересует игроков самого разного возраста. Сформулировать какие-либо четкие советы по поводу наивыгоднейшей стратегии игры здесь не просто, но все же позволим себе указать два важных правила:

1. Старайтесь играть так, чтобы на шахматной доске всегда оставалось место для четного числа пентамино (разумеется, если вы играете вдвоем).

2. Если вам не удается проанализировать создавшуюся позицию, постарайтесь по возможности усложнить ее так, чтобы противник оказался в еще более затруднительном положении, чем вы.

Наша следующая задача с пентамино совершенно не похожа на все предыдущие. Предположим, что вы хотите выпилить из листа фанеры все 12 пентамино, причем пила делает лишь прямые разрезы (другими словами, не может выпиливать углы). Какой наименьший (по площади) фанерный прямоугольник следует для этого взять? (U-пентамино, заштрихованное на рис. 19, потребует отдельного выпиливания - тут уж ничего поделать нельзя. Сначала вам придется выпилить гексамино - шестиклеточное полимино размером 2×3, а уж потом докончить его с помощью другой пилы.) Наилучшее решение здесь неизвестно, но заведомо можно обойтись прямоугольником размером 6×13. Для этого надо прежде всего, продвигаясь от сторон прямоугольника к его середине, пропилить жирные линии (см. рис. 19).

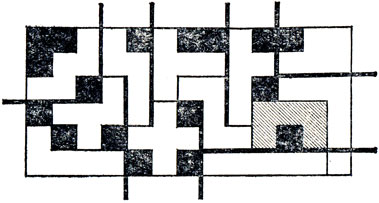
Рис. 19. Как вырезать 12 пентамино из прямоугольника 6×13

Вообще задачи с пентамино обладают одной замечательной и весьма поучительной особенностью. Допустим, у вас имеется какой-то материал и вы долго и безуспешно пытаетесь сложить из него определенный узор или фигуру. Добившись успеха, вы, естественно, сразу же решите, что ваш узор восхитителен, и это все, что можно соорудить из имеющегося у вас материала. Пентамино же показывает, как много различных и равноправно красивых узоров можно сложить из одного и того же материала так, что результат будет определяться не этим материалом, а лишь теми требованиями, которые мы перед собой поставим.

Но вполне возможно, что из заданного материала вообще нельзя сложить задуманных фигур. Проиллюстрируем сказанное на примере гексамино.