Гексамино

Существует 35 видов гексамино и 108 видов гептамино (семиклеточное полимино). Никто пока не нашел выражения или формулы для числа разных типов n-мино (n-клеточного полимино) как функции от n, то есть такой формулы, по которой можно было бы вычислить количество различных полимино, составленных из любого наперед заданного числа n сгруппированных квадратов. Подобные комбинаторные задачи на первый взгляд нередко кажутся обманчиво простыми, на самом же деле они очень сложны. О некоторых полученных в решении этой задачи результатах мы расскажем в гл. VI.

Все 35 гексамино покрывают площадь в 210 клеток. Вполне естественно постараться сложить их в прямоугольники размерами 3×70, 5×42, 6×35, 7×30, 10×21 или 14×15. Все эти попытки, однако, заведомо ни к чему не приведут. Доказательство - причем одно и то же сразу для всех наших прямоугольников - использует обычную шахматную раскраску доски, приводящую, очевидно, во всех шести случаях к 105 белым и 105 черным полям, то есть к нечетному числу полей каждого цвета. Из 35 гексамино 24 всегда покрывают три черные и три белые клетки (нечетное число тех и других), а остальные 11 - либо две белые клетки и четыре черные, либо же наоборот, другими словами, непременно четное число клеток каждого цвета. На рис. 20 а и 20 б изображены все 35 гексамино, расклассифицированные в соответствии с особенностями их "шахматной раскраски". Здесь мы имеем четное число - а именно 24 - "нечетных" гексамино и нечетное число - а именно 11 - "четных" гексамино. Поскольку из арифметики известно, что "четное количество нечетных чисел четно" и "нечетное количество, четных чисел также четно", все 35 гексамино в любом случае покроют четное число как белых, так и черных полей. В предложенных же прямоугольниках, если раскрасить их в шахматном порядке, как мы выяснили, количество черных (или белых) полей в точности равно 105. Это число нечетно, что и показывает невозможность покрытия любого из наших прямоугольников.

Рис. 20 а. 24 'нечетных' гексамино

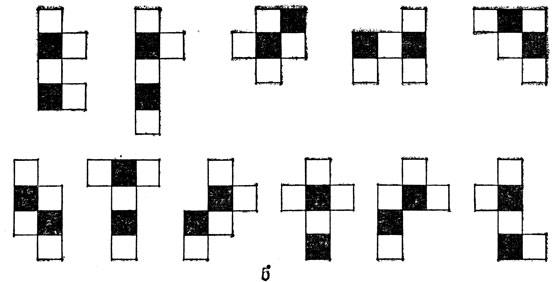
Рис. 20 б. 11 'четных' гексамино

Любопытно, что одна и та же раскраска шахматной доски - чередование черных и белых клеток - послужила для доказательства как очень простого факта о домино, так и гораздо более содержательной теоремы о гексамино. Очевидная идея использования этой раскраски заключается в "проверке на четность" числа полей разного цвета. В современной математике постоянно встречаются доказательства, опирающиеся на тот очевидный факт, что четное число никак не может быть равно нечетному^*. Раскрашиванию же полей просто помогает интуиция: поля разной раскраски мы никак не спутаем между собой. При этом часто, как, скажем, в задаче с прямыми тримино, раскраска сразу же выявляет решение, к которому мы могли бы прийти и другим путем, но ценой гораздо больших усилий.

^* (Ср., например, с используемыми в теории кодирования "проверками на четность", составляющими весьма важный прием обнаружения и исправления ошибок, вкравшихся при передаче сообщений по линиям связи (А. М. Яглом и И. М. Яглом, Вероятность и информация, М., изд-во "Наука", 1973; стр. 397 и след.).)