Тетрамино

Несколько теорем, относящихся к тетрамино (четырехклеточным полимино), несомненно, заслуживают упоминания, хотя подробные их доказательства мы опустим. При желании читатель может рассматривать приведенные ниже утверждения как задачи для самостоятельного решения,

1. Легко полностью покрыть шахматную доску прямыми тетрамино, или квадратными тетрамино, или Т-тетрамино, или L-тетрамино (рис. 7).

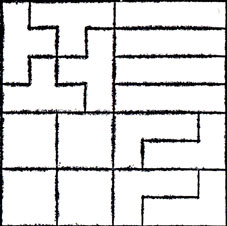
Рис. 7. Для покрытия шахматной доски можно использовать любое тетрамино, за исключением косого

2. Невозможно покрыть шахматную доску косыми тетрамино (их даже нельзя расположить на доске так, чтобы полностью покрывался ряд клеток, примыкающих к какой-либо одной стороне шахматной доски).

3. Невозможно покрыть шахматную доску 15 Т-тетрамино и одним квадратным тетрамино. (Это можно доказать, используя обычную раскраску шахматной доски: при такой раскраске каждое тетрамино всегда будет покрывать либо четное, либо, наоборот, нечетное число клеток каждого цвета.)

4. Невозможно также покрыть шахматную доску размером 8×8 с помощью 15 L-тетрамино и одного квадратного тетрамино. (Здесь самое простое доказательство использует покрытые точками и белые поля рис. 8.)

Рис. 8. Раскраска доски 8×8 для исследования ее покрытия L-тетрамино

5. Шахматную доску нельзя покрыть одним квадратным тетрамино и 15 другими, одни из которых (быть может, все) прямые, а остальные - косые. (Для доказательства можно использовать зигзагообразно заштрихованные и белые поля, изображенные на рис. 9.)

Рис. 9. Раскраска доски для исследования вопроса о ее покрытии прямыми и косыми тетрамино