Тримино

Ясно, что шахматную доску размером 8×8 нельзя целиком покрыть тримино - ведь 64 не делится на 3. Попытаемся вместо этого покрыть шахматную доску 21 тримино и одним мономино (просто квадратом).

Шахматную доску нельзя покрыть 21 прямым тримино и мономино, расположенным в нижнем левом углу доски. Для доказательства раскрасим шахматную доску, как показано на рис. 3. На рисунке мы имеем 22 заштрихованных поля, 21 белое и 21 черное поле. Но каждое прямое тримино независимо от того, как оно лежит на шахматной доске, всегда покрывает одно заштрихованное поле, одно белое и одно черное поле; поэтому 21 прямое тримино всегда покроет одинаковое число заштрихованных, белых и черных клеток доски. А так как нижний левый угол на рис. 3 - это черная клетка, то, если покрыть ее мономино, у нас останется только 20 черных клеток, зато будут 22 заштрихованные и 21 белая. Эти числа не равны; значит, покрыть оставшиеся 63 клетки прямыми тримино невозможно.

Рис. 3. Трехцветная раскраска шахматной доски

Отсюда сразу же следует и невозможность покрытия в случае, если мономино расположено в любом другом углу шахматной доски: ведь тогда мы сможет повернуть нашу доску так, чтобы мономино опять оказалось внизу слева, и далее придерживаться прежнего хода рассуждений. Все четыре угла шахматной доски совершенно равноправны между собой или симметричны - любой из них можно, поворачивая и зеркально отражая доску, перевести в любой другой. А если покрытие невозможно при одной конфигурации клеток, то оно невозможно и для любой конфигурации, симметричной первоначальной.

Вообще соображения симметрии бывают очень полезны в комбинаторной геометрии. Мы уже убедились (на примере задачи с мономино, расположенным в нижнем левом углу доски), что если мономино покрывает любую черную клетку, или любую белую клетку, или любую клетку, симметричную черной или белой, то оставшуюся часть шахматной доски нельзя покрыть прямыми тримино. Но единственные

заштрихованные клетки шахматной доски, для которых все симметричные им клетки тоже заштрихованные, - это те, которые показаны на рис. 4. Поэтому если мы расположим мономино на какой-нибудь клетке доски, отличной от этих четырех клеток, то оставшуюся часть шахматной доски прямыми тримино замостить наверняка нельзя. Таким образом, мономино может покрывать лишь одну из этих четырех клеток. А из рис. 5 следует, что эти четыре исключительные клетки и в самом деле являются исключительными: если расположить мономино на одной из них, то оставшуюся часть доски покрыть 21 прямым тримино можно.

Рис. 4. Заштрихованные поля не симметричны полям другого цвета на трехцветной шахматной доске

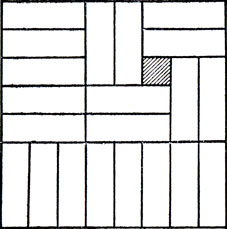
Рис. 5. Покрытие шахматной доски при помощи 21 прямого тримино и 1 мономино

Если обратиться ко второму типу тримино, то мы придем к иному результату: независимо от того, какую клетку шахматной доски покрывает мономино, оставшиеся клетки могут быть покрыты 21 прямоугольным (L) тримино.

Пусть сначала мы имеем шахматную доску размером 2×2. Ясно, что, где бы ни лежало на этой доске мономино, оставшиеся три клетки всегда можно покрыть прямоугольным тримино (рис. 6, а). Перейдем теперь к доске размером 4×4 и разобьем ее на четыре части размером 2×2 (рис. 6, б). Предположим, что мономино покрывает клетку, скажем, той из четырех частей, которая заштрихована на рис. 6, б. Так как каждая четверть доски представляет собой доску размером 2×2, то ее можно покрыть одним тримино и одним мономино, занимающим произвольную клетку этой доски. В заштрихованной части доски мономино уже есть; что же касается трех остальных четвертей, то мы расположим в них мономино на центральных (для большой доски) клетках. После этого мы сможем заменить наши три мономино на одно (прямоугольное) тримино (см. рис. 6, б). Окончательно мы покрыли шахматную доску размером 4×4 одним произвольно расположенным мономино и пятью прямоугольными тримино.

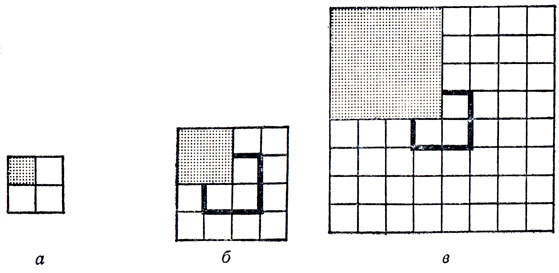
Рис. 6. Покрытие шахматной доски прямоугольными тримино

Случай доски размером 8×8 рассматривается аналогично. Поделим доску на четверти (доски размером 4×4; рис. 6, в). Произвольно расположенное мономино принадлежит одной из четвертей, и, согласно сказанному выше, мы можем завершить покрытие этой части прямоугольными тримино. Что касается трех оставшихся частей, то в них мы располагаем мономино на центральных (для большой доски) клетках и вновь, согласно сказанному ранее, сможем покрыть оставшиеся клетки этих частей прямоугольными тримино. После этого нам останется только заменить три занимающие центральные клетки мономино на одно прямоугольное тримино.

Приведенное доказательство основано на так называемом методе математической индукции - очень полезном приеме доказательства математических фактов^*. Первая доска имела размеры 2×2, что можно также записать в виде 2¹×2¹. (Число 2 называется основанием, а число 1 - показателем степени, в которую возводится основание, иными словами, числом раз, которое оно должно быть умножено само на себя. Так, 2¹, то есть 2 в первой степени, - это просто 2; 2² - это 2×2, или 4; 2³ - это 2×2×2, или 8; 2ⁿ - это 2 в степени n. Таким образом, доска размером 2×2 - это доска размером 2ⁿ×2ⁿ, где n = 1.) Случай доски размером 2×2 (то есть доски размером 2ⁿ×2ⁿ, где n = 1) оказался очень простым, а следующий случай доски 2ⁿ⁺¹×2ⁿ⁺¹ (например, доски размером 2¹⁺¹×2¹⁺¹ = 2²×2²=4×4) непосредственно следовал из предыдущего случая доски 2n×2n. Доказательства такого рода очень удобны для комбинаторного анализа; часто они помогают анализировать сложные геометрические конфигурации, повторяя и комбинируя более простые.

^* (См. И. С. Соминский, Л. И. Головина, И. М. Яглом, О математической индукции, М., изд-во "Наука", 1967.)